11. Вычисление интегралов вида Integrate[(Ax+B)/(Sqrt[ax^(2)+bx+c])dx]
![]()
1°. Замена переменной ![]() (универсальная тригонометрическая подстановка) интеграл такого типа приводит к интегралу от рациональной функции поскольку
(универсальная тригонометрическая подстановка) интеграл такого типа приводит к интегралу от рациональной функции поскольку ![]() ,
, ![]() и
и ![]() рационально выражаются через
рационально выражаются через ![]() :
:
|
|
|
|
|
| ||
2°. Поскольку существует замена, приводящая вычисление ![]() к вычислению интеграла от рациональной функции, то при любой функции
к вычислению интеграла от рациональной функции, то при любой функции ![]() интеграл вычисляется в элементарных функциях.
интеграл вычисляется в элементарных функциях.
3°. В некоторых частных случаях для функции ![]() Существуют более рациональные замены переменной, приводящие к интегрированию рациональной функции.
Существуют более рациональные замены переменной, приводящие к интегрированию рациональной функции.
1) ![]() нечетна по одной из переменных (например, по первой переменной
нечетна по одной из переменных (например, по первой переменной ![]() , то эта переменная может быть принята в качестве новой
, то эта переменная может быть принята в качестве новой ![]() ).
).
2) Если ![]() четна по паре переменных
четна по паре переменных ![]() , то походит замена
, то походит замена ![]() .
.
3°. Вычисление ![]() в случае, если хотя бы одно из чисел нечетно легко приводится к интегрированию многочлена:
в случае, если хотя бы одно из чисел нечетно легко приводится к интегрированию многочлена:
|
| |
|
|
Если оба числа – четные, то понижают степень, используя формулы:
![]() ,
, ![]() .
.
Примеры. Вычислить неопределенные интегралы
|
1) |
2) |
|
3) |
4) |
|
1) |
|
|
| |
|
| |
|
| |
|
| |
|
2) |
|
|
| |
|
| |
|
| |
|
3) |
|
|
| |
|
| |
|
| |
|
4) |
|
|
| |
|
|
Если степень ![]() достаточно большая и четная, метод приводит к длинным выкладкам и, кроме того, ответ получается в синус и косинусах кратных дуг, что не всегда удобно.
достаточно большая и четная, метод приводит к длинным выкладкам и, кроме того, ответ получается в синус и косинусах кратных дуг, что не всегда удобно.
В этих случаях удобнее пользоваться рекуррентными соотношениями для
![]() и
и ![]() .
.
Получим такую формулу для ![]() :
:
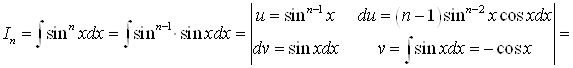
![]()
![]() ,
,
![]() .
.
Окончательно:
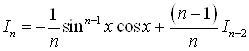 .
.
Аналогичная формула может быть получена для ![]()
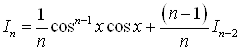 .
.
Вычислим по полученной формуле
![]()

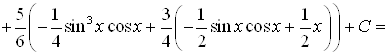
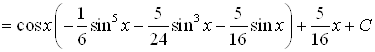 .
.
Интегралы типа ![]() ,
, ![]() для
для ![]() - четных легко вычисляются подстановкой
- четных легко вычисляются подстановкой 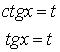
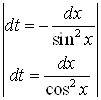 . При достаточно больших нечетных
. При достаточно больших нечетных ![]() лучше пользоваться рекуррентными соотношениями:
лучше пользоваться рекуррентными соотношениями:
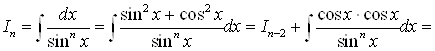

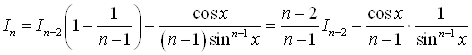
![]()
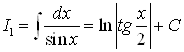
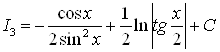
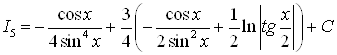
Интегралы вида 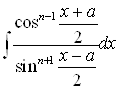 вычисляются заменой переменных:
вычисляются заменой переменных:
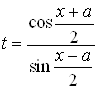
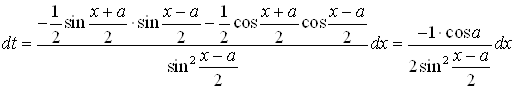
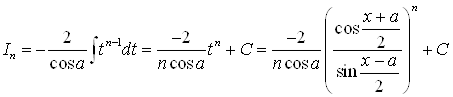
| < Предыдущая | Следующая > |
|---|
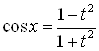 ;
;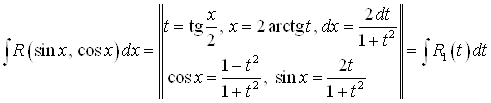 .
.

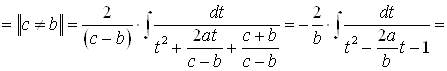

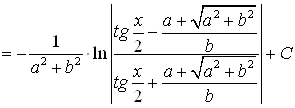 ;
;

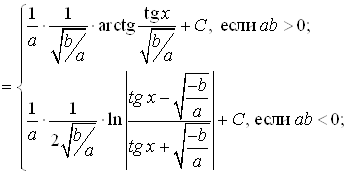 =
=
 ;
;
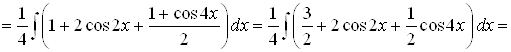
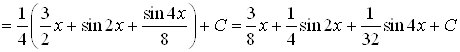 .
.