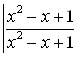09. Рациональные функции. Разложение на простейшие дроби. Интегрирование рациональной функции
1°. Рациональной дробью называют отношение двух многочленов:
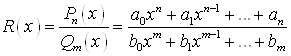 .
.
2°. Дробь ![]() называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе
называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе ![]() и неправильной, если
и неправильной, если ![]() .
.
3°. Любая неправильная дробь может быть представлена суммой многочлена и правильной дроби.
4°. Любая правильная дробь может быть разложена в сумму элементарных дробей I, II, III и IV типов, то есть в сумму дробей вида:
|
|
|
|
|
5°. Каждая из элементарных дробей интегрируется в элементарных функциях. Следовательно, любая рациональная дробь может быть проинтегрирована в элементарных функциях.
Для того чтобы разложить рациональную дробь на простейшие нужно:
1) Если дробь неправильная ![]() выделить целую часть, представив ее в виде суммы многочлена и правильной дроби.
выделить целую часть, представив ее в виде суммы многочлена и правильной дроби.
2) Знаменатель ![]() разложить на простейшие множители, то есть представить в виде:
разложить на простейшие множители, то есть представить в виде:
![]() ,
,
![]() .
.
3) Записать разложение с неопределенными коэффициентами. Каждому множителю вида ![]() в разложении соответствует сумма
в разложении соответствует сумма ![]() дробей первого и второго типа
дробей первого и второго типа
 ,
,
А каждому множителю вида ![]() в разложении соответствует сумма
в разложении соответствует сумма ![]() дробей третьего и четвертого типов
дробей третьего и четвертого типов
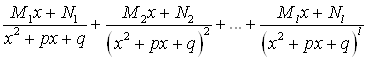 .
.
4) Для определения коэффициентов ![]() следует разложение привести к общему знаменателю. Полученная при этом дробь тождественно равна
следует разложение привести к общему знаменателю. Полученная при этом дробь тождественно равна 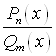 , и знаменатели у них совпадают. Значит, должны совпадать и числители.
, и знаменатели у них совпадают. Значит, должны совпадать и числители.
Уравнения для определения коэффициентов можно получить либо приравнивая коэффициенты при одинаковых степенях х, либо придавая переменной х последовательно значения вещественных корней знаменателя (если такие есть).
На практике для нахождения коэффициентов используют оба подхода одновременно.
Пример Вычислить интеграл
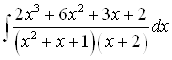 .
.
Решение Дробь под интегралом неправильная. Следует выделить целую часть
|
|
|
|
|
2) Знаменатель дроби уже разложен на простейшие множители;
|
3) |
|
|
|
4) Воспользуемся тем, что знаменатель имеет вещественный корень ![]() , подставим это значение в полученное равенство
, подставим это значение в полученное равенство
|
|
5) Приравнивая теперь коэффициенты при одинаковых степенях х, получим уравнения для определения остальных коэффициентов
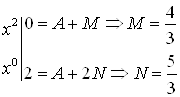
|
Итак, |
|
|
| |
|
| |
|
| |
В некоторых случаях интегрирование рациональных функций можно упростить. В частности, это касается вычисления интегралов вида:
А)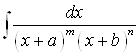 ;
;
Б)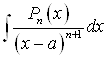 .
.
А) При вычислении интеграла  стандартным методом неопределенных коэффициентов приходится вычислять
стандартным методом неопределенных коэффициентов приходится вычислять ![]() коэффициентов и только 2 из них вычисляются легко, т. к корни знаменателя кратные. Сократить вычисления можно применив замену переменной:
коэффициентов и только 2 из них вычисляются легко, т. к корни знаменателя кратные. Сократить вычисления можно применив замену переменной:
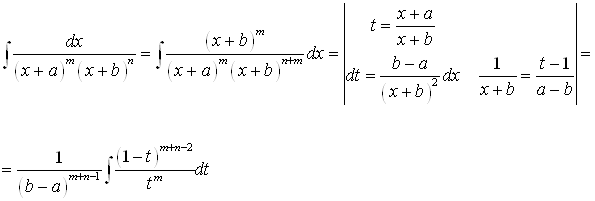
Используя такую замену, легко вычислить, например:

Б. Интегралы типа 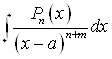 , где
, где ![]() - многочлен степени
- многочлен степени ![]() , а
, а ![]() , легко вычисляются, если
, легко вычисляются, если ![]() разложить по формуле Тейлора в т.
разложить по формуле Тейлора в т. ![]() .
.
Пример: Вычислить

Решение. Разложим ![]() по формуле Тейлора в т.
по формуле Тейлора в т. ![]()
Для этого следует вычислить
![]()
![]()
![]()
![]()
Тогда, в соответствии с формулой Тейлора ![]() ,
, 
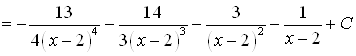 .
.
Для интегралов вида  метод неопределённых коэффициентов требует вычисления
метод неопределённых коэффициентов требует вычисления ![]() коэффициента и даже, если эти коэффициенты найдены, приводит к интегрированию выражений типа
коэффициента и даже, если эти коэффициенты найдены, приводит к интегрированию выражений типа 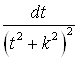 .
.
Этого можно избежать, если вычислять интеграл другим методом:
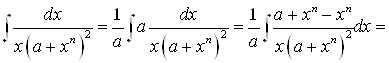
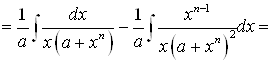

Если заметить, что
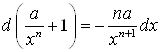 , а
, а ![]() ,
,
То оба интеграла легко вычисляются,
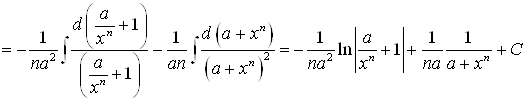 .
.
Пример: Вычислить 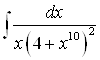
Решение.
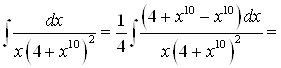


 .
.
Менее очевидно, но очень удачные подстановки, годятся для вычисления,
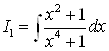 ,
,  ,
, 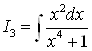 ,
, ![]() .
.
А) 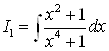 =
= .
.
Аналогично,

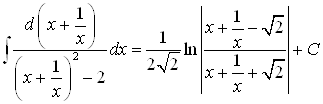 .
.
Интегралы ![]() и
и ![]() легко вычислить, если заметить, что
легко вычислить, если заметить, что ![]() , а
, а ![]() .
.
 ,
,
 .
.
Метод Остроградского интегрирования правильной рациональной дроби позволяет выделять рациональную часть интеграла без разложения знаменателя на произведение неприводимых множителей, и разложение рациональной дроби на простейшие. Формула Остроградского имеет вид:
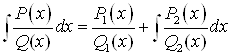
Здесь ![]() - наибольший общий делитель многочленов
- наибольший общий делитель многочленов ![]() и
и ![]() ;
; 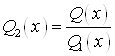 . Многочлены
. Многочлены ![]() и
и ![]() многочлены, степени на единицу меньше, чем соответственно
многочлены, степени на единицу меньше, чем соответственно ![]() и
и ![]() .
. ![]() и
и ![]() записывают с неопределенными коэффициентами. Эти коэффициенты можно вычислить, дифференцируя формулу Остроградского и сравнивая коэффициенты при одинаковых степенях в числителях.
записывают с неопределенными коэффициентами. Эти коэффициенты можно вычислить, дифференцируя формулу Остроградского и сравнивая коэффициенты при одинаковых степенях в числителях.
Пример: Методом Остроградского вычислить
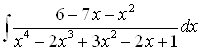 .
.
Решение:
Здесь ![]() ,
, ![]() .
.
Разделим ![]() на
на ![]() столбиком
столбиком
|
|
|
![]() делится без остатка на
делится без остатка на ![]() так же, как и
так же, как и ![]() . Таким образом, наибольший общий делитель многочленов
. Таким образом, наибольший общий делитель многочленов ![]() .
. ![]() можно найти разделив
можно найти разделив ![]() на
на ![]()
|
|
|
Формула Остроградского теперь принимает вид:
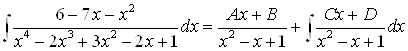 .
.
Для определения коэффициентов ![]() продифференцируем обе части формулы:
продифференцируем обе части формулы:
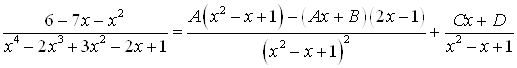
![]()
Сравнивая коэффициенты при одинаковых степенях получаем:

Решая систему получаем ![]() Таким образом:
Таким образом:
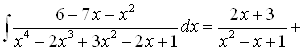
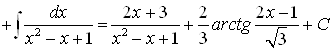 .
.
| < Предыдущая | Следующая > |
|---|
 ,
, ,
,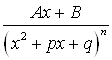 ,
, 

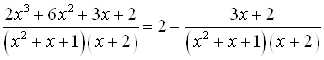 ;
; ;
;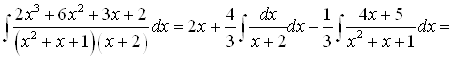
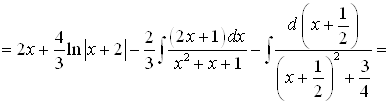
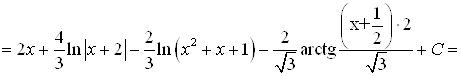
 .
.