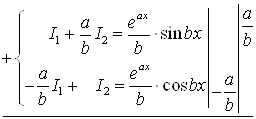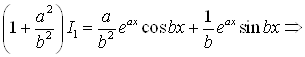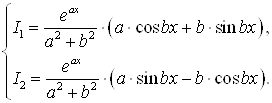07. Метод интегрирования по частям в неопределенном интеграле
Пусть функции 
и 
дифференцируемы на множестве Х и функция 
имеет первообразную на Х. Тогда функция 
тоже имеет первообразную и
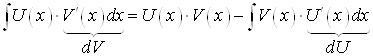
Чаще всего с помощью метода интегрирования по частям вычисляются интегралы вида:
|
1) |
2) |
3) |
|
4) |
5) |
6) |
|
7) |
;
;
;
;
;
;
.Здесь 
– многочлен степени 
. При вычислении интегралов первых четырех типов формулу интегрирования по частям приходится применять столько раз, какова степень многочлена, а для вычисления интеграла типа 7) раз.
Примеры. Вычислить неопределенные интегралы:
|
1) |
3) |
|
2) |
4) |
;
;
;
.|
1) |
|
|
| |
|
|
.В следующем примере степень многочлена 
и, метод интегрирования по частям придется применить дважды
|
2) |
|
|
| |
|
| |
|
| |
|
| |
|
3) |
|
|
| |
|
| |
|
4) |
|
|
| |
|
| |
|
|
;
;
.С помощью метода интегрирования по частям можно получить уравнение относительно исходного интеграла или рекуррентное соотношение.
Примеры. Вычислить неопределенные интегралы:
|
1) |
3) |
|
2) |
4) |
;
;
;
.1) Обозначим 
|
| |
|
| |
|
| |
|
| |
|
|
,
,
.Интегралы 2) и 3) можно вычислять одновременно.
|
| |
|
| |
|
|
,
.Таким образом, получаем систему:
|
| |
|
| |
|
|
Если степень многочлена достаточно высокая, то для вычисления интегралов вида:
1) 
2) 
3) 
Получим такие формулы.
А)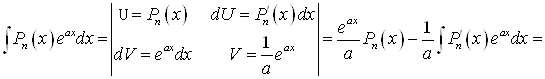 
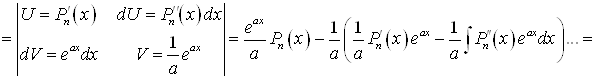
Используя полученную формулу, несложно вычислить, например,
.
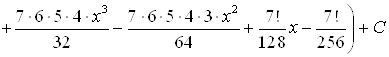Б)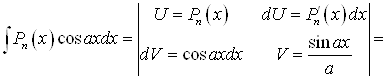 
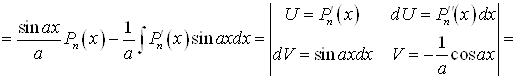
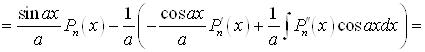
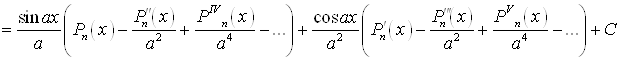
Аналогично может быть получена формула для 
Используя формулы (2) и (3) вычислим:
А) 
Б) 
А)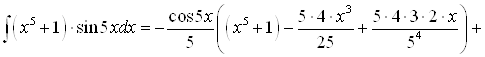 
.
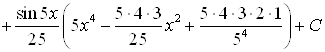Б) 
.
2. С помощью метода интегрирования по частям можно вывести так называемые рекуррентные формулы, дающие возможность свести некоторые интегралы к интегралам такого же типа, но более простым по структуре. Этот метод даёт возможность получить рекуррентную формулу для вычисления интеграла
.
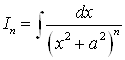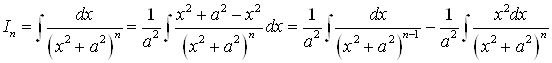
Ко второму интегралу применим метод интегрирования по частям
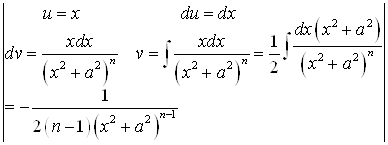
Тогда
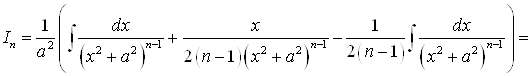
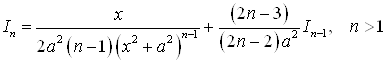
При 
Используя полученную формулу, легко вычислить, например
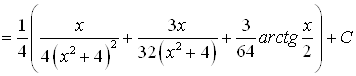
| < Предыдущая | Следующая > |
|---|
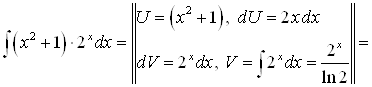
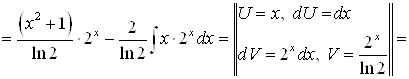
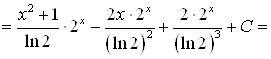
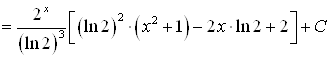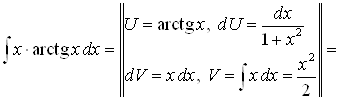
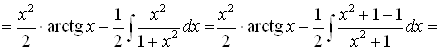
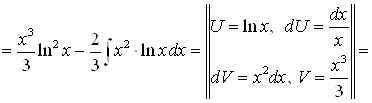
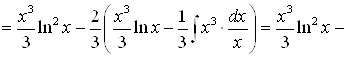
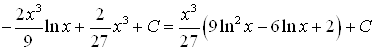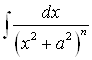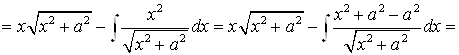
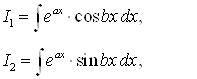
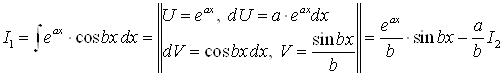