05. Замена переменной в неопределенном интеграле

1°. Пусть функция имеет обратную функцию и для функции известна первообразная тогда

.

Такой способ вычисления интегралов называют методом замены переменной или подстановки.

Обратите внимание, что между областями определения и при замене переменной должно быть взаимно-однозначное соответствие.

Примеры. Вычислить неопределенные интегралы:

1) ;	2) ;
3) ;	4) .

Решение.

1)
	;
2)
	;
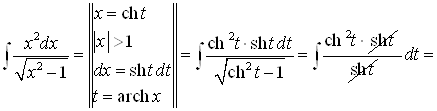
3)
	.

4) При вычислении интегралов типа 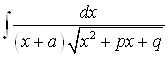целесообразно применять замену переменных ; .

В данном случае:

	.

< Предыдущая		Следующая >
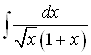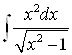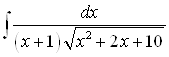
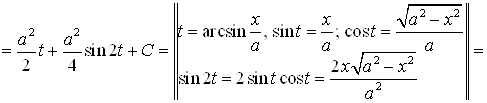
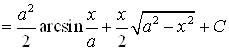
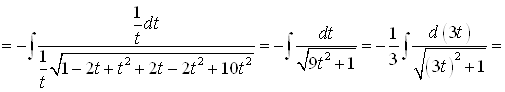
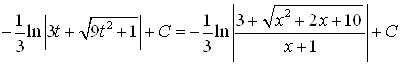