03. Метод подведения под знак дифференциала. Вычисление интегралов вида Integrate [(Ax+B)/(ax^(2)+bx+c)dx] и Integrate[(Ax+B)/(Sqrt[ax^(2)+bx+c])dx]

и

1°. Метод подведения под знак дифференциала основан на следующем утверждении:

Если , а – дифференцируемая функция, то

.

В частности

.

Для того чтобы применить это утверждение при вычислении интеграла, некоторые сомножители подынтегральной функции "подводят" под знак дифференциала, после чего используют подходящий табличный интеграл.

Примеры. Вычислить неопределенные интегралы:

1) ;	4) ;
2) ;	5) .
3) ;

Решение.

1)
	;
2)	;
3)	;
4)
	;
5)
	.

2°. Интегралы вида вычисляются по следующей схеме:

1) с помощью тождественных преобразований числитель представляют суммой двух слагаемых, одно из которых пропорционально производной знаменателя , а второе постоянно. В общем случае это выглядит так:

2) Первый из интегралов вычисляют подведением под знак дифференциала, второй после выделения полного квадрата в знаменателе приводится к одному из табличных интегралов или (это зависит от знака дискриминанта квадратного трехчлена).

Пример. Вычислить неопределенный интеграл .

Решение.

	.

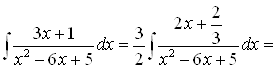
< Предыдущая		Следующая >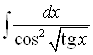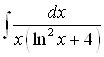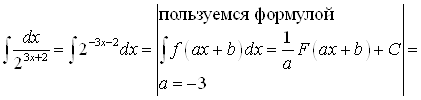
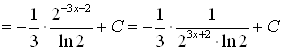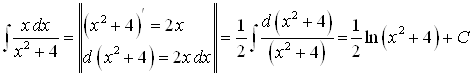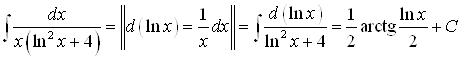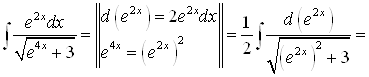
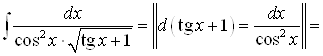
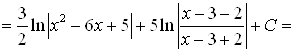