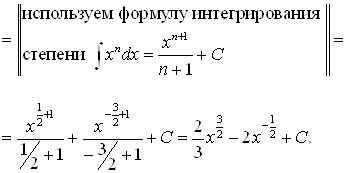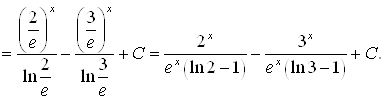01. Непосредственное интегрирование. Основные определения и формулировки
1°. Дифференцируемая функция 
называется первообразной для 
на некотором числовом множестве 
, если 
.
2°. Если 
и 
– первообразные на множестве X, то
.
3°. Если – первообразная на множестве X, то любая другая первообразная 
может быть представлена в виде
.
4°. Совокупность всех первообразных функции на множестве Х называется неопределенным интегралом и, обозначается
.
5°. Основные свойства неопределенного интеграла:
1) 
;
2) 
;
3) Операция интегрирования - линейна:
,
.
6°. Таблица неопределенных интегралов:
1) 
,
,
;
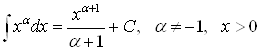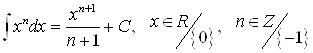2) 
;
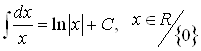3) 
;
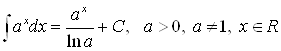4) 
;
5) 
;
6) 
;
7) 
;
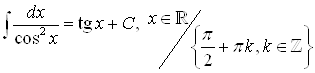8) 
;
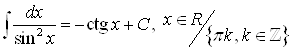9) 
;
10) 
;
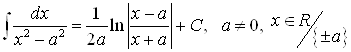11) 
;
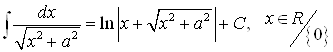12) 
;
13) 
;
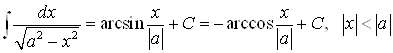14) 
;
15) 
;
16) 
;
17) 
.
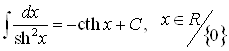Часто задачу интегрирования можно решить, используя только свойства неопределенного интеграла и таблицу интегралов. Этого достигают путем тождественных преобразований подынтегральной функции.
Примеры. Вычислить неопределенные интегралы:
|
1) |
2) |
3) |
;
;
.|
1) |
|
|
| |
|
2) |
|
|
| |
|
3) |
|
|
|
| Следующая > |
|---|
