17. Исчисление предикатов. Общезначимость

Описанная в предыдущем параграфе система по существу представляет собой исходную точку для формулирования различных исчислений предикатов. Отличительные особенности классического исчисления предикатов (которое мы рассматриваем) включают в себя дальнейшие предположения, распространяющие единственное допущение, сделанное в § 2.3 и относящееся к исчислению высказываний, а именно, что каждой простой формуле поставлено в соответствие только одно истинностное значение Т или F. Соответствующее допущение относительно простой формулы в исчислении предикатов гораздо сложнее. Мы введем его несколькими последовательными шагами.

Прежде всего примем, что системе, описанной в предыдущем параграфе, поставлено в соответствие непустое множество D, называемое полем, что каждая предметная переменная черпает свои значения в D. Примем, далее, что каждому л-местному предикатному символу поставлена в соответствие логическая функция, т. е. функция, определенная на D" со значениями в {Т, F}. (Для 0-местного предиката поставленную ему в соответствие функцию примем за постоянную Т или F). Примем, наконец, что простой формуле Р {у1, у2, ... , уn) приписывается истинностное значение, связанное с приписыванием элементов из поля D каждой переменной из числа у1, у2, ... , уn, следующим образом. Если переменной уi приписывается элемент di поля D и если предикатному символу P(x1, x2, ..., хn) приписывается значение : Dn → {Т, F}, то истинностное значение для Р (y1 у2, ... , уn) будет (D1, d2, ... , dn). Например, если Р(х, у, х) есть простая формула и формуле Р (х, у, z) приписывается значение , то истинностное значение Р (х, у, х), связанное с приписыванием элемента А переменной x и элемента b переменной у, будет (а, b, а).

В теории исчисления высказываний мы приняли, что не имеет значения, которое из двух истинностных значений Т и F приписывается простой формуле. В исчислении предикатов делается расширенное допущение, что теория не зависит от поля D и приписывания функций предикатным символам.

Вышеизложенное служит основой оценочной процедуры для формулы С в исчислении предикатов. В этой процедуре предполагается, что 1) дано поле D; 2) каждому предикатному символу, входящему в С, ставится в соответствие функция и 3) каждой из свободных переменных в С приписывается значение в D. Взятые вместе эти три положения задают приписывание для С. Истинностное значение, приписанное С, находится процедурой, которая аналогична образованию формулы С:

I) Если Р(Y1, y2, ... , yn) —простая формула, входящая в С, и формуле Р (х1: х.2, ..., хn) ставится в соответствие функция , а переменной yi приписывается di, то истинностное значение у Р(y1, y2, ... , yn) будет (d1, d2, ... , dn).

II) При данном приписывании значений предикатным символам и свободным переменным в ~А значение у~А есть F, если значение у А есть Т, и значение у~А есть Т. если значение у А есть F. Подобным же образом при данном приписывании значений предикатным символам и свободным переменным в формулах АВ, АВ, А→В и AВ применяются соответствующие истинностные таблицы исчисления высказываний.

III) При данном приписывании значений предикатным символам и свободным переменным в (х)А значение у(х)А есть Т, если значение А есть Т для каждого приписанного х значения, и значение у(х)А есть F, если значение А есть F по меньшей мере для одного приписанного х значения. При данном приписывании значений предикатным символам и свободным переменным в (Х) А значение у (Х)А есть Т, если значение у А есть Т по меньшей мере для одного значения х; в противном случае значение у (Эх)А есть F.

В качестве примера рассмотрим вопрос о приписывании истинностных значений формуле

(х)(Р(х)→Q)(QP(Y)).

Хотя поле D фиксировано, оно неизвестно. Предположим, что D = {a, b}. По предположению формуле Р(х) поставлена в соответствие логическая функция, определенная на D со значениями в {Т, F}, а формуле Q — некоторое истинностное значение. Далее, свободная переменная у может принимать любое значение в поле D. Логические функции, которые могут быть поставлены в соответствие формуле Р(х), даны ниже в таблице:

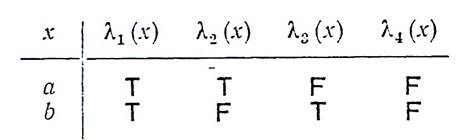
Значениями, которые можно поставить в соответствие формуле Q, являются Т и F, а у можно приписать значение а или b. Таким образом, мы можем внести в таблицу 16 (=4*2*2) записей, показывающих все возможные случаи распределения истинностных значении:

Значения, стоящие в столбцах под Р(х), Q и у в какой-либо данной строке, составляют приписываемые рассматриваемой формуле значения. Подробности вычисления, связанные, например, с приписыванием значений, внесенных в девятую строку таблицы, заключаются в следующем. Сперва мы подставляем приписываемые значения в формулу и получаем

(X)(3 (X)→T)(T3 (A)).

Чтобы приписать значение формуле (X)(3 (X)→T), мы должны вычислить 3(X)→T как логическую функцию х.

Соответствующая таблица дана ниже:

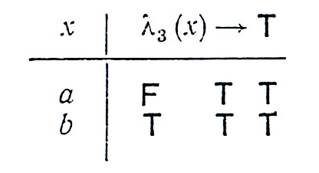
Поскольку истинностное значение импликации есть Т для всех значений, приписываемых х в D, (X)(3 (X)→T) получит значение Т. Поскольку 3(A)=F, формула T3(A) будет иметь значение F. Наконец, на основании таблицы для вся формула в целом получает значение Т. Резюмируем все шаги этого вычисления в табличной форме:

(x)(P(x)→Q) (QP(y)),

(x) 3(x)→Т) (Т3(a)),

T (TF),

T F

T

Мы стремимся дать такое описание исчисления предикатов, которое развивалось бы аналогично описанию исчисления высказываний, начиная с § 2.3. До сих пор мы ввели для исчисления предикатов символы, которыми будем пользоваться, дали определение формулы и описали оценочную процедуру. Следующий шаг в изложенной выше теории исчисления высказываний мы воспроизведем здесь в виде аналогичного определения общезначимости в исчислении предикатов. Формула общезначима в данном пом, если' она принимает значение Т при каждом приписывании значений предикатным символам и свободным переменным в ней. Формула общезначима, если она общезначима во всяком поле. Тот факт, что формула А общезначима, мы будем выражать так:

|=А

Уместно воспользоваться той же терминологией и теми же символами, что и раньше, поскольку приведенное определение общезначимости формулы представляет собой лишь расширение прежнего. Очевидно, при установлении общезначимости формулы истинностные таблицы должны уступить место процессам рассуждения. С другой стороны, для установления того, что формула не общезначима, достаточно будет одного поля D и одного приписывания, основанного на этом поле. Например, четвертая строка помещенной выше таблицы показывает, что рассматриваемая формула не является общезначимой. Легкость, с которой устанавливается, что некоторая формула не является общезначимой, может показаться читателю неожиданной.

Примеры А

1. Приведем пример, показывающий, как в исчислении предикатов предикатным символам ставятся в соответствие логические функции. Предположим, что Z — поле, и пусть нам известно, что Р (х, у, z) должно интерпретироваться как «z есть сумма х и y». Мы можем тогда поставить в соответствие этому предикатному символу функцию : Z3 → {Т, F} такую, что (а, b, с) = Т, если а+b=c, в противном же случае (а, b, c) = F. Если, с другой стороны, нам известно, что Р(х, у, z) должно интерпретироваться как «z есть произведение х и у», то мы припишем (а, b, с) значение Т, если ab = c, и значение F — в противном случае.

< Предыдущая		Следующая >