13. Исчисление высказываний. Логическое следствие
Во введении к этой главе было сказано, что задача логики — дать принципы рассуждения, т. е. теорию вывода. Практически это сводится к получению критериев для решения механическим путем вопроса о том, можно ли некоторую цепь рассуждений, основываясь на ее форме, считать правильной. Цепь рассуждений представляет собой просто конечную последовательность высказываний, приводимых в обоснование утверждения, что последнее высказывание в этой последовательности (заключение) может быть выведено из некоторых начальных высказываний (посылок). В обыденных условиях посылки вывода считаются истинными (на основании имеющегося опыта, эксперимента или убеждения). Если признать посылки вывода истинными, а принципы, использованные в цепи рассуждений, основанных на этих посылках, правильными, то мы вынуждены рассматривать полученное заключение как истинное. В математической теории дело обстоит иначе. Там мы интересуемся исключительно заключениями (так называемыми «теоремами» теории), которые можно вывести из принятой начальной системы высказываний (так называемых «аксиом» теории) в соответствии с правилами, установленными в какой-либо логической системе. В частности, в самой теории понятие истинности не играет никакой роли. Вклад исчисления высказываний в теорию вывода заключается в следующем: оно дает критерий вместе с практическими формами его применения для решения того, когда заключительному предложению рассуждения следует приписать истинностное значение Т, если каждой посылке этого рассуждения приписывается значение Т. Критерий этот имеет форму определения.
Высказывание В есть логическое следствие высказываний А1, А2,....., АM (в исчислении высказываний), что символически записывается в виде
А1, А2,....., АM |=B,
Если для всякого распределения истинностных значений, приписываемых каждой из простых формул Р1, Р2,....,.РN , входящих в одну или в несколько из формул А1, А2,....., АM и в В, формуЛа В получает значение Т всякий раз, как каждое Ai Получает значение Т. Если пользоваться истинностными таблицами, то «А1, А2,....., АM|=B» означает просто, что при построении истинностных таблиц для А1, А2,....., АM и В по перечню Р1, Р2,....,.РN простых формул, входящих в одну или в несколько из этих формул, В получает истинностное значение Т по меньшей мере для каждого приписывания отдельным Р истинностных значений, которое одновременно дает всем Ai значение Т.
Пример А
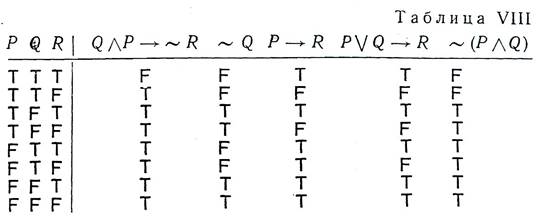
Рассматривая таблицу VIII, получаем следующие три иллюстрации к приведенному определению:
|=
, (строка 3)
|=
(строка 1 и 3)
|=
(строка 3, 7, 8)
Теорема 2.6. (I) А|=В тогда и только тогда, когда |= А→В.
(II) А1, А2,....., АM|= В тогда и только тогда, когда 
|=В, или тогда и только тогда, когда |=→B (M ≥ 2).
Доказательство. Докажем (I). Пусть А|= В. По таблице для →, А → В получает истинностное значение F тогда и только тогда, когда А получает значение Т и одновременно В получает значение F. На основании принятого допущения такая комбинация истинностных значений не встречается. Следовательно, А→В всегда получает значение Т, т. е. |= А → В. Для обратной теоремы пусть |= А → В; рассмотрим такое распределение истинностных значений, приписываемых простым компонентам, что А получает значение Т. Поскольку А → В получает значение Т, из таблицы для → следует, что В получает значение Т, откуда А|= В.
Первое из утверждений в (II) следует из таблицы для 
, а второе из первого, если использовать (I).
Следствие. А1, А2,....., АM-1, Am|= В тогда и только тогда, когда А1, А2,....., АM-1|=Am→B. В более общей форме: А1, А2,....., АM-1, Am|= В тогда и только тогда, когда |= A1 → (A2 →(…(Am → B) )).
Доказательство. При M = 1 первое утверждение есть (I) теоремы. Итак, примем, что А1, А2,....., АM-1, Am|= В при M > 1. Тогда |= 
на основании теоремы. Из тавтологии 8 теоремы 2.4 и следствия из теоремы 2.2 выводим, что |= 
. В соответствии с п. (I) теоремы находим, что |= 
, и, следовательно, на основании п. (II), 
|= 
Обратная теорема доказывается применением тех же операций в обратном порядке.
Наконец, второе утверждение получается последовательным применением первого.
Таким образом, вопрос о том, какие высказывания представляют собой логические следствия других высказываний (в исчислении высказываний), сводится к вопросу о том, какие высказывания общезначимы (этим объясняется важное значение тавтологий). С другой стороны, можно указать и прямые доводы в пользу нашего подхода к понятию логического следствия. Один из доводов заключается в возможности превратить определение в рабочий аппарат, напоминающий тот, какой применяется в математике для вывода теоремы из системы аксиом. Действительно, мы можем осуществить такой аппарат в виде последовательности формул (последняя формула представляет собой искомое заключение из посылок) таких, что наличие каждой из них обосновывается правилом, называемым правилом вывода (для исчисления высказываний). Основой для правил вывода, которые мы введем, служит следующая теорема.
Теорема 2.7. (I). 
|=
для i = 1, 2, ..., M.
(II). Если 
|= 
Для I = 1, 2, ..., P И если 
|= С, то |= C.
Доказательство. (I) непосредственно вытекает из определения «А1, А2,....., АM-1, Am|= В». Для доказательства (II) строим истинностную таблицу по перечню всех простых компонентов Р1, Р2,....,.РN,, входящих хотя бы в одну из формул А, В и С. Рассмотрим какой-нибудь ряд, в котором каждая формула А1, А2,....., АM-1, Am| получает истинностное значение Т. Тогда на основании сделанных допущений каждая формула В имеет значение Т и, следовательно, и С Имеет значение Т, т. е. при всяком распределении истинностных значений для Р, при котором каждое А получает значение Т, формула С Получает значение Т. Это и есть искомое заключение.
Основываясь на этом результате, можно представить доказательство того, что формула В (заключение) есть логическое следствие формул А1, А2,....., АM-1, AmТ (посылок), в виде цепочки (т. е. конечной последовательности) формул, последней из которых является В, и притом такой цепочки, что наличие в ней каждой из формул Е обосновывается применением одного из следующих правил.
Правило Р: формула Е есть посылка.
Правило T: формуле Е в цепочке предшествуют такие формулы А, .... С, что |=
Е.
Иными словами, мы утверждаем, что А1, А2,....., АM-1, Am|= В, если мы можем составить такую цепочку формул что каждая Е есть посылка (правило Р) или же в этой цепочке есть предшествующие формулы такие, что если С — их конъюнкция, то |= С
Е (правило T). В самом деле, примем, что каждое вхождение в рассматриваемую последовательность может быть оправдано указанным способом, и докажем, что тогда А1, А2, .... Am|= (любое Е в этой последовательности). На основании теоремы 2.7 (I) это верно в отношении E1. Примем, что каждая из формул 
K-1 ... Ek есть логическое следствие из формул А. Докажем, что то же верно и в отношении следующей формулы ЕK. Если ЕK есть посылка, то к ней применима теорема 2.7 (I). В противном случае существуют такие формулы, предшествующие ЕK, что если С — их конъюнкция, то |= C→EK. Пусть, скажем,
|= 
→ Ek,
Тогда по теореме 2.6 (II)
|= Ek,
И на основании принятого допущения
|= 
J = 1, 2, …, S.
Отсюда по теореме 2.7 (II)
А1, А2,....., Аm|= Ek.
Заметим, наконец, что, применяя правило T, можно ввести в вывод любую тавтологию. В самом деле, если |= D, то для всякой формулы А имеем |= A→D. Таким образом, D Можно включить в вывод, применяя правило T, в котором мы считаем какую-либо посылку формулой «A».
Примеры В
1. Докажем, что
|= 
Объяснение цифр, стоящих слева в нижеследующих строках, дано
Дальше:
{1} (1) A→C правило Р;
{1} (2) 
правило T; |= (1) - (2) на основании
тавтологии 11;
{3} (3) B→D Правило Р;
{3} (4) 
правило T; |= (3) - (4) на основании
тавтологии 11;
{1,3} (5) 
правило T; |= (2)(4)→(5) на основа-
нии тавтологии 7;
{6} (6) А
В правило P;
{1, 3, 6} (7) правило T; |= (5)(6)→(7) на основа-
нии тавтологии 1;
Цифры в круглых скобках рядом с каждой формулой обозначают и номер формулы, и номер строки вывода, в которую она входит. Номера в фигурных скобках в каждой строке соответствуют посылкам, от которых зависит формула в этой строке, т. е. формула в строке п есть логическое следствие из посылок, обозначенных номерами в фигурных скобках в этой строке. Так, формула в строке 5 есть логическое следствие посылок в строках 1 и 3, а формула в строке 7 есть логическое следствие посылок в строках 1, 3 и 6, т. е. всех посылок. В частности, в строке, заключающей в себе посылку, в фигурных скобках слева стоит как раз номер этой строки, поскольку такая формула не зависит от других строк. Фигурные скобки применены в номерах слева умышленно, так как такое обозначение напоминает о том, что формула в этой строке есть логическое следствие совокупности посылок, обозначенных этими номерами.
Перепишем теперь помещенный выше вывод, вводя при этом некоторые практические сокращения. Читателю предлагается в этой записи добавить номера использованных тавтологий:
{1} (1) A→С P
{1} (2) 
1 T
{3} (3) B→D P
{1, 3} (4) 
3 T
{6} (5) 
2, 4T
{1, 3, 6} (6) CD 5, 6T
| < Предыдущая | Следующая > |
|---|
