7.4. Метод Ньютона
Пусть известно приближение на K -м шаге Xk=![]() . Выпишем разложение функции Fi(X1, X2, …, Xn) по формуле Тейлора в точке Xk до второго порядка:
. Выпишем разложение функции Fi(X1, X2, …, Xn) по формуле Тейлора в точке Xk до второго порядка:

Тогда система (7.1) заменится системой уравнений:
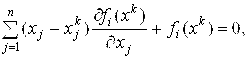 I=1, 2, …, N , (7.4)
I=1, 2, …, N , (7.4)
Линейной относительно приращений Xj-Xjk, J=1,2,…n. Решение X=(X1, X2,…, Xn)T системы (7.3) примем за следующее итерационное приближение и обозначим Xk+1 =![]() .
.
Таким образом, итерационный метод Ньютона для системы (7.1) определяется системой уравнений:
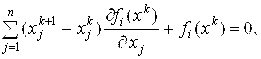 I=1, 2, …, N , (7.5)
I=1, 2, …, N , (7.5)
Из которой последовательно, начиная с заданного X0=( X10, X20, …, Xn0)T, находятся векторы Xk, K=1,2,…. . Систему (7.4) можно записать в векторном виде:
![]() K=1, 2, …,
K=1, 2, …,
Где X0 - заданный вектор, F΄ (X) - матрица Якоби.
 (7.6)
(7.6)
Если обозначить Zk=Xk+ 1- Xk и если (F΄(Xk))-1 существует, то, решив систему линейных алгебраических уравнений:
F΄ (Xk) Zk = - F(Xk),
(K+1) - е приближение найдем из формулы
Xk+1=zk + xk.
Условие остановки итерационного процесса можно взять в виде
![]() или
или ![]() .
.
| < Предыдущая | Следующая > |
|---|