7.1. Решение систем нелинейных алгебраических уравнений. Определения

Система нелинейных уравнений представляется в следующем виде:

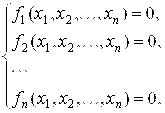(7.1)

Где Fi (i=1, 2,…, N ) - Функции вещественных переменных X1, X2, …, Xn. Обозначим упорядоченную совокупность N Чисел X = ( X1, X2, …, Xn)TÎH И F(X) = (F(X1),F( X2), …, F(Xn))T. Тогда система уравнений (7.1) в некотором линейном пространстве H размерности N запишется в операторном виде: F(X)=0, где F:H® H нелинейное отображение. Такие системы решают итерационными методами.

Многие одношаговые итерационные методы для решения системы F(X)=0 можно записать в канонической форме:

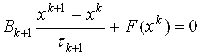. (7.2)

Где K - номер итерации Xk = ( Xk1, Xk2, …, Xkn)T, TK+1 - числовой параметр, - матрица N X N, Имеющая обратную матрицу.

Метод (7.2) называется Явным, если Bk+1 =E Для всех K, и Неявным в противном случае.

< Предыдущая		Следующая >