2.7. Кубический сплайн

Построим на отрезке [A,B] функцию Si(X) так, чтобы на каждом отрезке

[X i-1 , x i ] (I=1,...,n) функция Si(X) представляла собой полином третьей степени

Si(X)=ai+ bi (Xi-x) +Ci(Xi-x)2+Di(Xi-x)3

И в узлах Xi имела первую и вторую непрерывные производные:

(X)= - bi - ci(Xi-x) - Di(Xi-x)2,

(X)=Ci+Di(Xi-X),

(A) ==0.

Используя условие интерполирования и непрерывности, имеем:

Si(Xi)= f(Xi),

Si(Xi)= Si+1(Xi),

(Xi)= (Xi),

(Xi)= (Xi),

Далее, обозначив Yi=f(Xi) и Hi+1=xi+1-xi, получим, что

Ai=yi, (2.1)

ai=ai+1+bi+1hi+1+Ci+1+Di+1, (2.2)

bi=bi+1+ci+1hi+1 +Di+1, (2.3)

ci=Ci+1+Di+1Hi+1. (2.4)

Из (2.4) следует:

Di+1=(I=0,1,..N-1). (2.5)

Подставим (2.5) в (2.2) и выразим Bi+1:

Bi+1=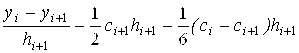(I=0,1,…N-1). (2.6)

Подставим (2.6) и (2.5) в (2.3) и получим систему из (N-1) трехточечного уравнения относительно переменной C:

αI Ci-1 +βI Ci+ γI Ci+1 = φI , (I=1,…,n-1), (2.7)

Где

αI = hi,

βI = 2(Hi+1+hi),

γI = Hi+1,

φI = 6.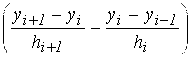

Уравнение (2.7) при краевых условиях ((A) ==0) c0=0, cn=0 Решается методом прогонки:

Ci = pi+1 ci+1 + qi+1 (I=n-1,…,1). (2.8)

Запишем формулу (2.8) для Ci-1 И подставим в уравнение (2.7):

αi (Pi ci + qi ) +βi ci + γici+1 =φi.

Выразим отсюда Ci:

Ci=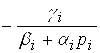Ci+1+.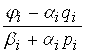

Сравнивая с формулой (2.8), выпишем формулы для прогоночных коэффициентов Pi+1 И qi+1:

Pi+1=,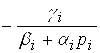

Qi+1=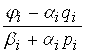 (I=1,…, N-1).

Для вычисления P1 , q1 Запишем краевое условие C0=0 В виде (2.8):

С0=p1c1+q1=0.

Отсюда следует, что P1=0, q1=0. Определим все Pi+1, QI+1 Для I=1,…N-1 И, зная граничное условие Cn=0 по (2.8) для I=N-1,…,1, найдем все Ci.. Затем из формул (2.5) и (2.6) получим оставшиеся коэффициенты для кубического сплайна.

< Предыдущая		Следующая >