07. Табличный метод
Обозначим через ![]() ,
, ![]() базисные переменные, а через
базисные переменные, а через ![]() ,
, ![]() свободные. Выразив целевую функцию и базисные переменные через свободные, сформулируем задачу в следующем виде: максимизировать
свободные. Выразив целевую функцию и базисные переменные через свободные, сформулируем задачу в следующем виде: максимизировать ![]() (7) при условных
(7) при условных ![]() ,
, ![]() ,
,![]() ,
, ![]() (8). Тогда задачу можно представить следующей матрицей:
(8). Тогда задачу можно представить следующей матрицей:
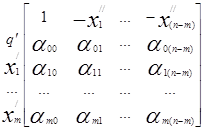 (9)
(9)
Замечая, что столбец коэффициентов αi 0, i≠0 представляет собой базисное решение при базисе ![]() , а строка α0j, j≠0 представляет собой взятые с обратным знаком коэффициенты при свободных переменных в выражении q/, приходим к выводу, что базисное решение допустимо если αi 0≥0, i≠0. Если α0j≥0, j≠0, то она является и оптимальной. При оптимальном базисном решении
, а строка α0j, j≠0 представляет собой взятые с обратным знаком коэффициенты при свободных переменных в выражении q/, приходим к выводу, что базисное решение допустимо если αi 0≥0, i≠0. Если α0j≥0, j≠0, то она является и оптимальной. При оптимальном базисном решении ![]() .
.
Рассмотрим наш пример:
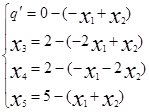
Матрица коэффициентов в виде таблиц:
А)
|
1 |
|
| |
|
Q/ |
0 2 |
-1 1 |
1 -2 |
|
|
2 4 |
-2 2 |
1 -4 |
|
|
2 2 |
1 -1 |
-2 -2 |
|
|
5 -2 |
1 -1 |
1 2 |
Б)
|
1 |
|
| |
|
Q/ |
2 1 |
1 -1/3 |
1 -1/2 |
|
|
6 3 |
2 -1 |
3 1 |
|
|
2 2 |
1 -2/3 |
-2 2/3 |
|
|
3 1 |
-1 -1/3 |
-1 -1/3 |
В)
|
1 |
|
| |
|
Q/ |
3 |
2/3 |
1/3 |
|
|
9 |
1 |
1 |
|
|
4 |
1/3 |
2/3 |
|
|
1 |
-1/3 |
1/3 |
Т. к α0i отрицательно, то оптимум не найден, значит переменную х, следует сделать базисной. Если отрицательными окажутся α0j при нескольких свободных переменных, то в базисном можно переводить любую из них.
Определим каждую из базисных переменных. Нужно сделать свободной ту, которая быстрее обратится в нуль при увеличении х1. Это будет та базисная переменная хi, для которой коэффициенты в столбце αi1>0 и отношение ![]() наименьшее. Это переменная хn.
наименьшее. Это переменная хn.
Коэффициент αi1 стоящий на пересечении столбца х1 и строки xn назовем генеральным. Пусть ![]() λ =1 выделим коэффициенты, стоящие на строке х1 и столбце xn. Теперь заполним нижние правые углы клеток:
λ =1 выделим коэффициенты, стоящие на строке х1 и столбце xn. Теперь заполним нижние правые углы клеток:
1) в клетку αi1 заполняем λ.
2) в клетках выделенной строки записываем верхние коэффициенты, умноженные на + λ.
3) В клетках выделенного столбца записываем верхние коэффициенты, умноженные на - λ.
4) В остальных клетках записываем произведение выделенных коэффициентов, на пересечении которого стоит данная клетка.
Заполним таблицу Б:
1) Строку и столбец соответствующие новым свободной и базисной переменой, заполняем нижними коэффициентами выделенной строки и столбца таблицы а.
2) В остальные клетки записываем суммы коэффициентов стоящих в соответствующих клетках таблицы а.
Оптимальное решение не найдено – повторим процедуру, заполняя таблицу b. Теперь коэффициенты α0j, j≠0 положительны, и она даёт оптимальное решение, которое находим по столбцу свободных членов: x1=4; x2=1; x3=9; x4=x5=0; ![]() ;
; ![]() .
.
| < Предыдущая | Следующая > |
|---|