1. Геометрическая интерпретация основной задачи планирования производства и графический способ ее решения
Задача оптимального планирования является самой важной из задач линейного программирования. Если сформулировать задачу линейного программирования без экономической интерпретации, то она такова: найти экстремум линейной функции при линейных же ограничениях на переменные. При этом множество значений переменных, удовлетворяющих всем ограничениям задачи, называется допустимым множеством. Допустимое множество представляет собой некоторое многогранное тело в линейном числовом пространстве размерности, равной числу переменных задачи. Линейная же функция, экстремум которой ищется, называется целевой функцией.
В случае двух переменных задача планирования производства имеет наглядную геометрическую интерпретацию.
Дана задача линейного программирования:
|
C=с1x1+c2x2®min (max) |
(1) |
|
|
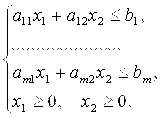
(2) |
Необходимо среди допустимых решений системы (2) найти то, которое обращает в минимум (максимум) линейную целевую функцию (1).
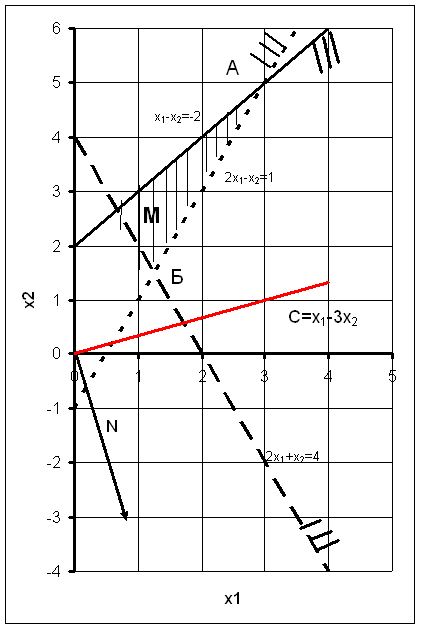
Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой ![]() (i=1,2,…,m). Если система совместна, полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых составляют решение данной системы. Совокупность этих точек называют многоугольником решений.
(i=1,2,…,m). Если система совместна, полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых составляют решение данной системы. Совокупность этих точек называют многоугольником решений.
При графической интерпретации задачи линейного программирования могут встретиться следующие случаи.
1. Целевая функция достигает своего экстремума в одной угловой точке многоугольника решений (в его вершине).
2. Целевая функция достигает своего экстремума на отрезке – это происходит тогда, когда линия уровня целевой функции параллельна одной из сторон выпуклого многоугольника, причем эта сторона расположена в направлении смещения линии уровня при стремлении целевой функции к своему оптимуму. В этом случае задача будет иметь бесчисленное множество решений.
3. Целевая функция не достигает своего экстремума, т. к. область решения представляет собой незамкнутый многоугольник
4. Разговор о нахождении экстремума целевой функции не ведут, т. к. система ограничений задачи несовместна, а область решения есть пустое множество.
Схема графического метода решения задачи состоит из следующих этапов.
1. Записываются уравнения граничных прямых;
2. Строятся графики граничных прямых на координатной плоскости;
3. Находится область определения каждого из неравенств системы;
4. Строится многоугольник решений;
5. Строится график целевой функции и направляющий вектор N;
6. Определяется экстремальная точка многоугольника
7. Вычисляется значение целевой функции в полученной точке.
Рассмотрим алгоритм решения на конкретном примере.
ПРИМЕР:
Решите графическим методом задачу линейного программирования:
C=x1-3x2®min

1. Уравнения граничных прямых: 1)x1-x2=-2; 2)2x1+x2=4; 3)2x1-x2=1; 4)x1=0; 5)x2=0.
2. Строятся в декартовой системе координат графики граничных прямых (рис.1)
3. Определяется область решения для каждого из неравенств. С этой целью выбирают любую точку плоскости декартовой системы координат и подставляют значения координат х1 и х2 этой точки в неравенство, область
|
Рис. 1. Графическая иллюстрация решения задачи линейного программирования |
Решения которого отыскиваем. Если координаты выбранной точки (х1,х2) удовлетворяют неравенству, то решением его является та полуплоскость, где лежит эта точка. Если же координаты данной точки не удовлетворяют неравенству, то областью решения является противоположная полуплоскость. Определим область решения для неравенства x1-x2³-2. Возьмем точку с координатами (0;0), подставим значение координат х1=0 и х2=0 в неравенство, получим 0³-2, областью определения данного неравенства является полуплоскость содержащая точку с координатами (0;0),что и показано штриховкой на рис.1. Аналогично определяем области решения для остальных неравенств системы. |
4. Строится многоугольник решений. Областью решения системы пяти неравенств в данном случае будет треугольник М, ограниченный данными тремя граничными прямыми.
5. Строится линия уровня целевой функции и направляющий вектор N. Направляющий вектор выходит из начала координат к точке с координатами коэффициентов при целевой функции, т. е. в нашем примере к точке с координатами (1;-3). Вектор N показывает направление возрастания целевой функции, он всегда перпендикулярен линии уровня целевой функции, поэтому строим прямую проходящую через начало координат и перпендикулярную вектору N. Это и будет линия уровня целевой функции.
6. Определяется экстремальная точка многоугольника. В рассматриваемом примере необходимо найти минимум целевой функции, поэтому следует перемещать линию уровня целевой функции параллельно самой себе в направлении противоположном вектору N до тех пор пока линия уровня не станет опорной прямой. Крайнее положение в треугольнике М прямая занимает в двух точках Б и А. В точке Б будет максимум целевой функции, а в А – минимум.
Координаты искомой точки при хорошем качестве построения можно определить по чертежу, если это сделать трудно (координаты представляют собой дробные числа) необходимо их вычислить аналитически, решив совместно систему уравнений граничных прямых, пересечение которых образует искомую точку. В нашем случае необходимо решить следующую систему уравнений:
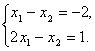
Точка А имеет координаты (3;5)
7. Вычисляется значения целевой функции в полученной точке
Сmin=3-3*5=-12
| Следующая > |
|---|