04. Открытая модель транспортной задачи. Дополнительные условия в постановке

На практике часто возникают задачи транспортного типа, которые отличаются от стандартной модели. Некоторые из таких отличий перечисляются ниже вместе с рекомендациями по их обработке. Также приводится пример.

1. Если количество груза в пунктах отправления больше, чем в пунктах назначения, то вводится фиктивный потребитель лишней продукции. Если потребности в товарах больше, чем его имеется, то вводится фиктивный отправитель недостающего груза. Стоимости перевозок по фиктивным маршрутам устанавливаются равными нулю. Модель становится закрытой.

2. Если товар по какому-то маршруту не должен перевозится (запрещенная перевозка), то стоимость перевозки по данному маршруту устанавливается равной . Другими словами, если необходимо , то .

3. Если по данному маршруту необходимо перевезти заданное количество груза (), то устанавливаются новые значения

4. Если количество груза должно быть не меньше заданного количества (), то устанавливаются , а стоимость перевозки не изменяется.

5. Если количество груза должно быть не больше заданной величины (), то устанавливается новый столбец с потребностями , стоимости перевозок по всем маршрутам копируются из -го столбца. В самом -м столбце перевозка по маршруту (, ) запрещается, устанавливается и изменяется потребность .

1. В условиях открытой модели может быть организовано приоритетное обслуживание. Допустим, что у отправителей груза больше, чем потребности в нём. При этом груз из -го пункта должен быть выведен полностью. Вводится фиктивный потребитель груза, как в пункте 1. Стоимости перевозок в столбце фиктивного потребителя устанавливаются равными нулю, за исключением -той строки. Здесь стоимость перевозки равна бесконечности. Аналогично поступают, когда суммарные потребности в грузе больше, чем имеется у отправителей, и заявка одного из пунктов назначения должна удовлетворяться полностью.

Рассмотрим пример.

Условия перевозки грузов заданы в таблице 1. При перевозке должны выполнятся следующие дополнительные условия:

1) ;

2) ;

3) потребности второго пункта назначения должны удовлетворяться полностью. Требуется так организовать перевозку, чтобы её стоимость была минимальной.

Таблица 1

Решение: Составим таблицу 2, руководствуясь следующими соображениями:

1. Поскольку суммарная потребность в грузах >, то вводится фиктивный отправитель груза , третья строка в таблице 2. Стоимости перевозок равны нулю, за исключением , поскольку потребности второго пункта назначения должны удовлетворятся полностью;

2. Согласно требованию устанавливаем ;

3. Согласно требованию устанавливаем:

1) дополнительный столбец , в котором стоимости перевозок те же, что и в третьем столбце исходной задачи;

2) :

3) .

Таблица 2

	5	25	15	10
10	4	1	3	3	0
30	8	3		10 1	2
15	0		0	0	-3
	6	1	3	-1

Для составления опорного плана используем метод минимального элемента, более эффективный, чем метод северо-западного угла. Для этого в таблице 2 находим ячейку с наименьшей стоимостью перевозок, если их несколько, то выбираем ту, в которой можно перевести наибольший груз. В нашем случае это ячейка (3,3), груз 15 ед. Исключаем из рассмотрения 3-й столбец и 3-ю строку таблицы, и на оставшихся ячейках снова находим наименьшую стоимость и перевозим максимальный груз. Это ячейка (1,2), груз 10 ед. Исключаем из рассмотрения 1-ю строку, по маршруту (2,4) перевозим 10 ед. груза, по маршруту (2,2) – 15 ед., (2,1) – 5 ед.

Находим потенциалы и разности

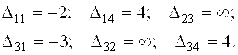
Поскольку и отрицательны, то план таблицы 3 не является оптимальным. Составим цикл, вершины которого помечены символами (+) или (-).

Начинается цикл в вершине (3,1), поскольку <. Наименьшая со знаком (-) перевозка равна 5 ед. Добавляем и вычитаем 5 в соответствующих вершинах цикла.

Таблица 3

	5	25	15	10
10	4	5 1	5 3	3	0
30	8	20 3		10 1	2
15	5 0		10 0	0	-3
	3	1	3	-1

Переходим к таблице 3

Поскольку все , то найденный опорный план является оптимальным.

Таблица 4

Переходим к таблице 4, которая соответствует исходным условиям задачи. Убеждаемся, что дополнительные условия удовлетворены. По таблице 4 находим стоимость перевозок

(ед.)

< Предыдущая		Следующая >