07. Методы спуска

С помощью рассмотренного метода циклического покоординатного спуска выполняется одномерный поиск из заданной точки в направлении, параллельном одной из координатных осей, до точки минимума в данном направлении. Затем одномерный поиск производится в направлениях, параллельных другим осям. Все направления поиска в этом методе фиксированы. Целесообразно модифицировать этот метод таким образом, чтобы на каждом этапе одномерный поиск производился вдоль «наилучшего направления», обеспечивающего наиболее быстрое убывание функции. Важной концепцией методов многомерной минимизации является понятие о направлении спуска.

Вектор называется Направлением спуска функции в точке , если существует такое , что для всех .

Пусть функция дифференцируема и задан вектор . Тогда производная функции в точке по направлению определяется как предел

. (1.12)

В частности, если , то является направлением спуска. Поэтому на основании (1.12) используют еще одно определение.

Пусть – дифференцируемая функция при . Если существует вектор , такой что , то называется Направлением спуска функции в точке .

Действительно, при помощи формулы Тейлора

Легко видеть, что существует , такое, что для всех , если и только если является направлением спуска функции в точке , то есть .

Методы многомерной минимизации функций, в которых используются направления спуска, называются Методами спуска.

Методы спуска являются итерационными методами. Для выполнения первой итерации задается начальная точка . Итерации выполняются по формуле

, (1.13)

Где – номер итерации, ; – скалярное значение, определяющее шаг поиска; – направление спуска. Итерации продолжаются до тех пор, пока не выполнится критерий окончания процесса минимизации

, (1.14)

Где – допустимая погрешность, .

Во всех методах спуска используется формула (1.13). Различные методы спуска отличаются выбором направления спуска и способом определения шага поиска .

Во многих методах шаг поиска вычисляется как такое значение переменной , которое доставляет минимум функции одной переменной . Используя необходимое условие минимума дифференцируемой функции скалярного аргумента, получим, что в точке минимума должно выполняться равенство . Но это означает, что равна нулю производная (1.12) функции в точке по направлению

. (1.15)

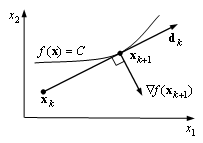
Это необходимое условие точного одномерного поиска. Таким образом, в методах спуска с применением точного одномерного поиска градиент функции в конечной точке итерации ортогонален направлению поиска в этой итерации (рис. 1.8).

Итерация метода спуска (1.13) с проведением точного одномерного поиска представляется в виде:

, . (1.16)

Рис. 1.8. Точный одномерный поиск

Эти формулы будут использоваться в последующих численных методах многомерной безусловной минимизации, представленных в данном пособии и отличающихся лишь выбором направления спуска. Любой метод спуска можно описать общим алгоритмом, основанным на формулах (1.16), (1.14).

Алгоритм метода спуска.

Входные параметры: – начальная точка поиска, – процедура вычисления функции, – допустимая погрешность.

Выходной параметр – конечная точка поиска.

1. Вычислить направление спуска в точке .

2. Вычислить , .

3. Положить .

4. Если , то перейти к шагу 1.

5. Остановиться.

В этом алгоритме на шаге 2 выполняется одномерный поиск минимума из текущей точки поиска в направлении спуска . Для повышения эффективности одномерного поиска производят масштабирование направления поиска и используют вектор направления единичной длины. Шаг перехода в следующую точку поиска обозначен через вектор . Итерации продолжаются, пока длина больше заданной допустимой погрешности.

< Предыдущая		Следующая >