05. Условия оптимальности второго порядка

Необходимое условие оптимальности первого порядка в общем случае не является достаточным условием оптимальности, поскольку стационарная точка не обязана быть решением задачи безусловной минимизации (1.1). Для анализа стационарных точек применяются условия оптимальности второго порядка, основанные на вторых производных целевой функции.

Пусть функция является дважды дифференцируемой и существует матрица вторых частных производных целевой функции – Матрица Гессе

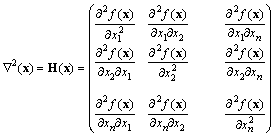. (1.8)

В силу теоремы Шварца

, , .

Поэтому матрица Гессе (1.8) – симметрическая матрица и для нее

. (1.9)

Для строго выпуклой функции матрица Гессе является положительно определенной матрицей, а для строго вогнутой функции матрица Гессе отрицательно определенная.

Для выявления лишних стационарных точек может использоваться необходимое условие оптимальности второго порядка.

Теорема 1.4. Пусть функция дважды дифференцируема в точке . Тогда, если – точка локального минимума функции , то матрица Гессе этой функции в точке неотрицательно определена:

, . (1.10)

Доказательство. Разложим функцию в окрестности точки в ряд Тейлора, ограничиваясь слагаемыми не выше второго порядка малости,

.

Тогда с учетом (1.6) при достаточно малых имеем

.

Разделив обе части неравенства на и переходя к пределу при , получим (1.10). ÿ

Достаточное условие локальной оптимальности содержит характерное усиление требований к матрице Гессе.

Теорема 1.5. Пусть функция дважды дифференцируема в точке . Тогда, если и матрица Гессе функции в точке положительно определена, то есть

, , , (1.11)

То – точка строгого локального минимума функции .

Доказательство. Доказательство проведем от противного. Предположим, что существуют точки, близкие к точке , со значением функции, не большим, чем в точке . Составим из них последовательность , удовлетворяющую условиям:

, , .

Представим в виде , где , . Поскольку , то без ограничения общности можно считать, что . Составим ряд Тейлора, ограничиваясь слагаемыми не выше второго порядка малости

.

Тогда с учетом (1.6) имеем

.

Разделив обе части неравенства на и переходя к пределу при , получим противоречие с (1.11). ÿ

Для функции скалярного аргумента условия (1.10) и (1.11) означают, что вторая производная неотрицательна и положительна соответственно.

Заметим, что необходимые условия оптимальности, представленные теоремами 1.2 и 1.4, не являются достаточными. Например, для функции эти условия выполнены в точке перегиба , которая не является точкой минимума. Условия теоремы 1.5 не являются необходимыми для оптимальности. Для функции эти условия не выполнены в точке строгого минимума , поскольку и .

В тех случаях, когда функция достаточно проста, теоремы 1.2, 1.3 и 1.4 позволяют явно решить задачу (1.1). При этом для исследования матрицы на положительную и отрицательную определенность, как правило, используется критерий Сильвестра – Якоби.

Теорема 1.6. Пусть является стационарной точкой функции , для которой , и пусть в этой точке и в некоторой ее окрестности функция имеет непрерывные частные производные первого и второго порядков. Тогда:

1) если определитель матрицы Гессе

И все его главные диагональные миноры , , …, положительны, то в точке функция имеет минимум;

2) если определители , , …, , имеют соответственно знаки –, +, –, +, …, то в точке функция имеет максимум;

3) если , а числа , , …, , ни положительны, ни знакочередуются по закону –, +, –, +, …, то в точке функция не имеет экстремума.

Примечание 1.1. Теорема 1.6 решает задачу исследования функции нескольких переменных на экстремум не полностью. Возможен случай, когда . В этом случае полный дифференциал второго порядка , и тогда разность эквивалентна полному дифференциалу функции третьего порядка, исследование которого, вообще говоря, намного сложнее. В этом случае вопрос о наличии экстремума в точке остается открытым и требует дополнительного исследования.

Пример 1.3. Для квадратичной функции (1.3) имеем:

, .

Необходимое условие оптимальности первого порядка приводит к системе уравнений: , . Решая эту систему, получим стационарную точку . Определитель матрицы Гессе и его главный диагональный минор положительны:

, .

По теореме 1.6 найденная точка – точка минимума функции (1.3), что совпадает с ранее полученным результатом в примере 1.1.

Пример 1.4. Для функции Розенброка (1.4) получим:

,

.

Градиент и матрица Гессе функции Розенброка зависят от вектора . Необходимое условие экстремума дает систему уравнений: , . Решением этой системы найдем стационарную точку , в которой

.

Определитель матрицы Гессе и его главный минор положительны:

, .

Следовательно, – точка минимума функции (1.4), ранее найденная в примере 1.2.

< Предыдущая		Следующая >