1.1. Перестановки. Размещения. Сочетания

Пусть есть некоторое конечное множество элементов U={A1, A2, ..., AN}. Рассмотрим набор элементов , где ÎU, J = 1, 2, ..., R.

Этот набор называется выборкой объема R из N элементов. Любое подмножество U является выборкой, но не всякая выборка является подмножеством U, так как в выборку один и тот же элемент может входить несколько раз (в отличие от подмножества).

Комбинаторные задачи связаны с подсчетом числа выборок объема r из n элементов, где выборки подчиняются определенным условиям, т. е. выбор производится по какому-нибудь принципу. Подсчет числа выборок основывается на двух правилах теории множеств.

Принцип суммы: если card A = M, card B = N и AÇB = Æ , то card A È B = =M+N. На комбинаторном языке это означает: если объект A можно выбрать M способами, объект B другими n способами и их одновременный выбор невозможен, то выбор “A или B” может быть осуществлен M+N способами.

Принцип произведения: если card A=M, card B=N, то card (A´B)=M+N. На комбинаторном языке это означает: если объект A может быть выбран M способами, при любом выборе A объект B может быть выбран N способами, то выбор “A и B” может быть осуществлен M×N способами.

Пример 1. A = 10 {различных шоколадок}, B = 5 { различных пачек печенья}. Выбор “A или B” означает, что выбирается что-то одно и способов выбора в этом случае будет 15. Выбор “A и B” означает, что выбирается 1 шоколадка и 1 пачка печенья и различных вариантов для такого выбора будет 50.

Пример 2. Бросают 2 игральные кости. Сколькими способами они могут выпасть так, что на каждой кости выпадет четное число очков либо на каждой кости выпадет нечетное число очков?

Пусть M – число возможностей для выпадения четного числа на одной кости, N – число возможностей для выпадения нечетного числа. Здесь M = N = 3. По правилу произведения количество выпадения четных чисел, как и нечетных, равно 9. По правилу суммы количество возможностей для выпадения двух четных и двух нечетных чисел будет 18.

Рассмотрим основные способы формирования выборок.

Определение. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Если порядок следования элементов несущественен, то выборка называется неупорядоченной.

Из определения следует, что две упорядоченные выборки, состоящие из одних и тех же элементов, но расположенных в разном порядке, являются различными.

Перестановки. Упорядоченные выборки, объемом N из N элементов, где все элементы различны, называются перестановками из N элементов. Число перестановок из N элементов обозначается Pn.

Теорема. P = N!

Доказательство проводится по индукции. Очевидно, если N = 1, то перестановка только одна и P1 = 1!. Пусть для N = K теорема верна и Pk = K!, покажем, что она тогда верна и для N = K+1. Рассмотрим (K+1)- й элемент, будем считать его объектом A, который можно выбрать K+1 способами. Тогда объект B – упорядоченная выборка из оставшихся K элементов по K. B соответствии с индуктивным предположением объект B можно выбрать K! способами. По принципу произведения выбор A и B можно осуществить K!(K+1) = (K+1)! способами. Совместный выбор A и B есть упорядоченная выборка из K + 1 элементов по K + 1.

Пример 3. Сколько существует способов, чтобы расположить на полке 10 различных книг? Ответ: 10!

Можно рассуждать иначе. Выбираем первый элемент, это можно сделать N способами. Затем выбираем второй элемент, это можно сделать (N - 1) способами. По правилу произведения упорядоченный выбор двух элементов можно осуществить N´(N - 1) способами. Затем выбираем третий элемент, для его выбора останется N - 2 возможности, последний элемент можно выбрать единственным способом. Мы вновь приходим к формуле: N(N - 1)(N - R) ... 1.

Размещения. Упорядоченные выборки объемом M из N элементов (M < N), где все элементы различны, называются размещениями. Число размещений из N элементов по M обозначается .

Теорема. =

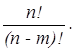
Обозначим X = . Тогда оставшиеся (N – M) элементов можно упорядочить (N – M)! способами. По принципу произведения, если объект A можно выбрать X способами, объект B (N – M)! способами, то совместный выбор “A и B” можно осуществить X ×(N – M)! способами, а выбор “A и B” есть перестановки и Pn = N! Отсюда X = =

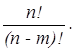
Рассуждая иначе: первый элемент выбираем N способами, второй – (N – 1) способами и т. д. , M–й элемент выбираем (N – M + 1) способом. По принципу произведения вновь имеем: N(N – 1)...(N – M +1), что совпадает с .

Пример 4. Группа из 15 человек выиграла 3 различных книги. Сколькими способами можно распределить эти книги среди группы?

Имеем = 15 ×14 ×13 = 2730.

Сочетания. Неупорядоченные выборки объемом M из N элементов (M < N) называются сочетаниями. Их число обозначается .

Теорема.

Доказательство. Очевидно, Действительно, объект A – неупорядоченная выборка из N элементов по M, их число . После того, как эти M элементов отобраны, их можно упорядочить M! способами (в роли объекта B выступает “порядок“ в выборке). Совместный выбор “A и B“ – упорядоченная выборка.

Пример 5. Группа из 15 человек выиграла 3 одинаковых книги. Сколькими способами можно распределить эти книги?

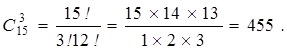
Сочетания, размещения и перестановки являлись подмножествами исходного множества. Рассмотрим выборки, которые не являются подмножествами.

Размещения с повторениями. Упорядоченные выборки объемом M из N элементов, где элементы могут повторяться, называются размещениями с повторениями. Их число обозначается (N).

Теорема. (N) = Nm.

Доказательство. Первый элемент может быть выбран N способами, второй элемент также может быть выбран N способами и так далее, M - й элемент также может быть выбран N способами. По принципу произведения получаем Nm .

Пример 6. Кодовый замок состоит из четырех разрядов, в каждом разряде независимо от других могут быть выбраны цифры от 0 до 9. Сколько возможных комбинаций?

Здесь N = 10, M = 4 и ответом будет 104.

Пример 7. Рассмотрим вектор длины M, каждая координата которого может принимать всего 2 значения: 0 или 1. Сколько будет таких векторов?

Это есть выборка, объемом m из двух элементов. Ответ: 2M

Перестановки с повторениями. Пусть имеется N элементов, среди которых K1 элементов первого типа, K2 элементов второго типа и т. д., Ks элементов S-го типа, причем K1 + K2 + ... + Ks = N. Упорядоченные выборки из таких N элементов по N называются перестановками с повторениями, их число обозначается CN(K1, K2, ..., Ks). Числа CN(K1, K2, ..., KS) называются полиномиальными коэффициентами.

Теорема. Cn(K1, ..., Ks)=

Доказательство проведем по индукции по S, т. е. по числу типов элементов. При S = 1 утверждение становится тривиальным: K1 = N, все элементы одного типа и CN(N) = 1. В качестве базы индукции возьмем S = 2, N = K1 + K2. В этом случаем перестановки с повторениями превращаются в сочетания из N элементов по K1 (или K2): выбираем K1 место, куда помещаем элементы первого типа.

Cn(K1,K2) =

Пусть формула верна для S = M , т. е. N = K1 + ... + Km и

Cn(K1, ..., Km)=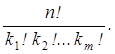

Докажем, что она верна для S = M + 1 (N = K1 +... + Km + Km+1). В этом случае перестановку с повторениями можно рассматривать как совместный выбор двух объектов: объект A – выбор K m + 1 места для элементов (M + 1)-го типа; объект B – перестановка с повторениями из (N – Km+1) элементов. Объект A можно выбрать способом, B – (K1, ..., KM) способами. По принципу произведения

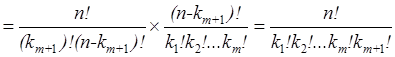
И мы получили требуемую формулу.

Замечание. Числа 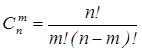называются биноминальными коэффициентами. Из этой формулы следует, что

Пример 8. Сколько различных слов можно получить, переставляя буквы в слове “математика”?

Решение. Буква “а” входит 3 раза (K 1= 3), буква “м” – 2 раза (K2 = 2), “т” – 2 раза (K3 = 2), буквы “е”, ”к”, ”и” входят по одному разу, отсюда K3 = K4 = K5 = 1.

C10 (3, 2, , 2, 1, 1, 1) = 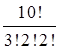=151200.

Сочетания с повторениями. Пусть имеется N типов элементов, каждый тип содержит не менее M одинаковых элементов. Неупорядоченная выборка объемом m из имеющихся элементов (их число ³ M´N ) называется сочетанием с повторением. Число сочетаний с повторениями обозначается (N).

Теорема. (N) = .

Доказательство. Пусть в выборку вошло M1 элементов первого типа, M2 элементов второго типа, ...MN – N-го типа. Причем каждое 0 £ M i£ M и M1+M2+ ...+ Mn= =M. Сопоставим этой выборке вектор следующего вида: Очевидно, между множеством неупорядоченных выборок с повторениями и множеством векторов {Bn} существует биекция (докажите это!). Следовательно, (N) равно числу векторов Bn. “ Длина вектора” Bn равна числу 0 и 1, или M+ +N–1. Число векторов равно числу способов, которыми M единиц можно поставить на M + N - 1 мест, а это будет .

Пример 9. В кондитерской имеется 7 видов пирожных. Покупатель берет 4 пирожных. Сколькими способами он может это сделать? (Предполагается, что пирожных каждого вида ³ 4).

Число способов будет

Пример10. Пусть V = {A, B, C}. Объем выборки M = 2. Перечислить перестановки, размещения, сочетания, размещения с повторениями, сочетания с повторениями.

1. Перестановки: {Abc, Bac, Bca, Acb, Cab, Cba}. P3=3!=6.

2. Размещения: {(Ab), (BC), (Ac), (Ba), (Cb), (Ca)}.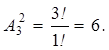

3. Сочетания: {(Ab), (Ac), (Bc)}.

4. Размещения с повторениями: {(Ab), (Bc), (Ac), (Ba), (Cb), (Ca), (Aa), (Bb), (Cc)}. (3)= 32 = 9.

5. Сочетания с повторениями: {(Ab), (Bc), (Ca), (Aa), (Bb), (Cc)}.

< Предыдущая		Следующая >