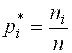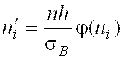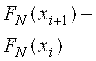23. Методические указания к выполнению задания № 5
Математическая статиcтика изучает массовые явления и процессы, ставя целью получение выводов по данным наблюдений за ними. В результате появляются утверждения об общих характеристиках таких явлений в предположении постоянства начальных условий явления. Теоретической основой математической статистики является теория вероятностей.
Поскольку число наблюдений конечно, их результаты можно записать в таблицу аналогично дискретной случайной величине, только в нижней строке не вероятности, а частоты тех или иных значений, а чаще – диапазонов. При этом при анализе такой таблицы нередко возникает предположение, что данная величина распределена по одному из известных непрерывных законов (см. комментарии к задаче № 4), чаще всего – нормальному (гауссовскому).
Типовой пример
Получены статистические данные (N=500) зависимости результатов измерения роста студентов (Х) от окружности груди (Y). Измерения проводились с точностью до 1 см.
Таблица 1
Статистические данные типового примера
|
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
X |
172 |
172 |
163 |
187 |
172 |
161 |
176 |
164 |
166 |
168 |
162 |
163 |
|
Y |
88 |
91 |
89 |
99 |
90 |
85 |
88 |
84 |
82 |
82 |
82 |
89 |
…………..
|
N |
489 |
490 |
491 |
492 |
493 |
494 |
495 |
496 |
497 |
498 |
499 |
500 |
|
X |
165 |
173 |
166 |
175 |
158 |
174 |
178 |
170 |
167 |
168 |
161 |
161 |
|
Y |
85 |
89 |
84 |
98 |
83 |
86 |
90 |
86 |
93 |
94 |
89 |
88 |
Требуется:
1 часть.
1) произвести выборку из 200 значений;
2) построить эмпирическую функцию распределения, полигон, гистограмму для случайной величины Х;
3) построить точечные и интервальные оценки для мат. ожидания и дисперсии генеральной совокупности Х;
4) сделать статистическую проверку гипотезы о законе распределения случайной величины Х;
Часть 2.
1) нанести на координатную плоскость данные выборки (X;Y) и по виду корреляционного облака подобрать вид функции регрессии;
2) составить корреляционную таблицу по сгруппированным данным;
3) вычислить коэффициент корреляции;
4) получить уравнение регрессии;
1) Произведём из генеральной совокупности N=500 выборку N=200 значений. Для этого воспользуемся таблицей случайных чисел (Приложение А). Выберите столбец, номер которого соответствует месяцу Вашего рождения. В этом столбце отсчитайте порядковый номер даты дня рождения. В полученном случайном числе определите номера ещё трёх столбцов. Для данного примера выбрана дата 31 декабря. В 12 столбце определили 31 номер случайного числа. Это число 0436. Значит выбранными будут столбцы №12;4;13;16. (№12 – месяц Вашего рождения, №4 – первая или вторая цифра в случайном числе, которая не использовалась, №13 – третья цифра в случайном числе +10, №16 – четвёртая цифра в случайном числе +10). Если цифры повторяются, то нужно взять со3седние номера. Например, случайное число во втором столбце - 4422. Нужно выбрать номера 2,4,12,13.
Для осуществления выборки берутся последние три цифры в случайном числе, которые определяют порядковый номер выборочного значения. Если в выборке встретился номер, которого нет в генеральной совокупности, то необходимо вычислить разность между этим числом и 500. Если полученный номер уже выбрали, то необходимо выбрать следующий за ним номер.
Для представленного примера получилась выборка:
Таблица 2
Выборочные данные X и Y
|
N |
106 |
493 |
66 |
201 |
274 |
158 |
223 |
336 |
362 |
162 |
96 |
20 |
|
X |
162 |
166 |
172 |
169 |
176 |
167 |
167 |
168 |
167 |
169 |
167 |
69 |
|
Y |
100 |
84 |
82 |
91 |
86 |
90 |
92 |
88 |
89 |
88 |
89 |
83 |
|
N |
288 |
251 |
257 |
152 |
279 |
478 |
86 |
439 |
368 |
203 |
271 |
395 |
|
X |
169 |
163 |
164 |
164 |
164 |
178 |
176 |
167 |
165 |
172 |
168 |
170 |
|
Y |
91 |
92 |
84 |
89 |
85 |
91 |
82 |
85 |
90 |
87 |
88 |
88 |
|
N |
396 |
94 |
305 |
341 |
12 |
128 |
492 |
407 |
172 |
87 |
441 |
29 |
|
X |
187 |
165 |
171 |
171 |
169 |
163 |
161 |
175 |
172 |
163 |
180 |
172 |
|
Y |
86 |
87 |
94 |
91 |
79 |
80 |
88 |
95 |
89 |
91 |
98 |
90 |
|
N |
140 |
59 |
70 |
453 |
487 |
447 |
105 |
232 |
95 |
456 |
80 |
225 |
|
X |
174 |
164 |
169 |
157 |
178 |
176 |
161 |
176 |
165 |
161 |
182 |
176 |
|
Y |
97 |
89 |
88 |
90 |
90 |
93 |
94 |
90 |
87 |
84 |
90 |
93 |
|
N |
147 |
101 |
373 |
51 |
343 |
355 |
195 |
463 |
260 |
183 |
326 |
282 |
|
X |
168 |
164 |
160 |
178 |
170 |
168 |
173 |
176 |
170 |
163 |
165 |
165 |
|
Y |
93 |
91 |
83 |
89 |
90 |
81 |
89 |
95 |
81 |
93 |
84 |
88 |
|
N |
139 |
483 |
399 |
467 |
266 |
372 |
356 |
290 |
241 |
273 |
450 |
329 |
|
X |
170 |
166 |
165 |
181 |
172 |
165 |
172 |
178 |
173 |
165 |
174 |
159 |
|
Y |
86 |
84 |
85 |
92 |
88 |
91 |
98 |
90 |
90 |
87 |
96 |
81 |
Продолжение таблицы 2
|
N |
469 |
423 |
242 |
475 |
168 |
365 |
107 |
428 |
367 |
457 |
224 |
199 |
|
X |
171 |
169 |
169 |
170 |
170 |
165 |
190 |
175 |
157 |
148 |
172 |
159 |
|
Y |
92 |
92 |
87 |
91 |
88 |
94 |
105 |
91 |
82 |
87 |
99 |
83 |
|
N |
404 |
363 |
192 |
109 |
429 |
60 |
13 |
291 |
400 |
337 |
100 |
187 |
|
X |
162 |
167 |
167 |
160 |
175 |
163 |
164 |
180 |
164 |
169 |
169 |
170 |
|
Y |
92 |
85 |
88 |
87 |
90 |
91 |
89 |
85 |
84 |
87 |
91 |
93 |
|
N |
88 |
292 |
283 |
52 |
45 |
358 |
252 |
62 |
130 |
286 |
361 |
184 |
|
X |
179 |
167 |
162 |
169 |
172 |
166 |
164 |
173 |
161 |
159 |
166 |
158 |
|
Y |
99 |
81 |
80 |
91 |
99 |
82 |
84 |
84 |
82 |
86 |
84 |
91 |
|
N |
79 |
371 |
378 |
419 |
307 |
56 |
374 |
169 |
43 |
298 |
239 |
145 |
|
X |
163 |
165 |
170 |
172 |
161 |
171 |
166 |
164 |
183 |
173 |
166 |
167 |
|
Y |
88 |
87 |
91 |
94 |
84 |
97 |
87 |
97 |
90 |
90 |
89 |
85 |
|
N |
325 |
65 |
153 |
375 |
9 |
340 |
142 |
193 |
261 |
116 |
26 |
253 |
|
X |
162 |
156 |
167 |
168 |
170 |
171 |
174 |
179 |
161 |
170 |
172 |
166 |
|
Y |
89 |
88 |
86 |
92 |
90 |
91 |
90 |
85 |
79 |
95 |
91 |
88 |
|
N |
61 |
202 |
440 |
21 |
200 |
221 |
332 |
275 |
287 |
108 |
468 |
103 |
|
X |
173 |
172 |
179 |
155 |
175 |
173 |
170 |
171 |
171 |
167 |
165 |
173 |
|
Y |
89 |
96 |
85 |
86 |
89 |
96 |
96 |
83 |
90 |
91 |
91 |
90 |
|
N |
240 |
110 |
424 |
414 |
296 |
284 |
83 |
435 |
81 |
54 |
397 |
134 |
|
X |
167 |
165 |
169 |
171 |
181 |
164 |
164 |
176 |
163 |
165 |
174 |
177 |
|
Y |
89 |
94 |
82 |
89 |
89 |
86 |
91 |
87 |
88 |
93 |
86 |
87 |
|
N |
303 |
430 |
34 |
144 |
277 |
451 |
179 |
472 |
342 |
293 |
327 |
448 |
|
X |
180 |
170 |
168 |
175 |
171 |
170 |
168 |
160 |
169 |
164 |
171 |
164 |
|
Y |
90 |
91 |
82 |
85 |
89 |
90 |
87 |
85 |
91 |
87 |
91 |
83 |
|
N |
154 |
438 |
297 |
219 |
196 |
204 |
230 |
258 |
262 |
213 |
89 |
357 |
|
X |
164 |
163 |
170 |
174 |
161 |
167 |
173 |
164 |
174 |
168 |
176 |
156 |
|
Y |
83 |
88 |
92 |
88 |
91 |
91 |
87 |
90 |
91 |
83 |
93 |
85 |
|
N |
426 |
480 |
156 |
127 |
295 |
115 |
36 |
7 |
473 |
376 |
157 |
254 |
|
X |
162 |
168 |
176 |
184 |
165 |
176 |
163 |
167 |
169 |
186 |
172 |
175 |
|
Y |
90 |
93 |
88 |
98 |
94 |
92 |
89 |
88 |
89 |
92 |
91 |
90 |
|
N |
98 |
126 |
265 |
443 |
82 |
110 |
432 |
479 |
|
X |
170 |
173 |
160 |
171 |
169 |
165 |
185 |
168 |
|
Y |
90 |
91 |
89 |
85 |
87 |
94 |
91 |
90 |
Составим ранжированный (по увеличению) ряд для случайной величины Х.
Таблица 3
Ранжированный ряд случайной величины Х
|
X |
148 |
155 |
156 |
156 |
157 |
157 |
158 |
159 |
159 |
159 |
160 |
160 |
|
Y |
87 |
86 |
85 |
88 |
82 |
90 |
91 |
81 |
83 |
86 |
83 |
85 |
|
X |
160 |
161 |
161 |
161 |
161 |
161 |
161 |
162 |
162 |
162 |
162 |
162 |
|
Y |
87 |
79 |
82 |
84 |
84 |
88 |
91 |
80 |
89 |
90 |
92 |
94 |
|
X |
162 |
163 |
163 |
163 |
163 |
163 |
163 |
163 |
163 |
163 |
164 |
164 |
|
Y |
100 |
80 |
88 |
88 |
88 |
89 |
91 |
91 |
92 |
93 |
83 |
83 |
|
X |
164 |
164 |
164 |
164 |
164 |
164 |
164 |
164 |
164 |
164 |
164 |
164 |
|
Y |
84 |
84 |
84 |
85 |
86 |
87 |
89 |
89 |
89 |
90 |
90 |
91 |
|
X |
164 |
164 |
165 |
165 |
165 |
165 |
165 |
165 |
165 |
165 |
165 |
165 |
|
Y |
91 |
97 |
84 |
85 |
87 |
87 |
87 |
87 |
88 |
90 |
91 |
91 |
|
X |
165 |
165 |
165 |
165 |
165 |
166 |
166 |
166 |
166 |
166 |
166 |
166 |
|
Y |
93 |
94 |
94 |
94 |
94 |
82 |
84 |
84 |
84 |
87 |
88 |
89 |
|
X |
166 |
167 |
167 |
167 |
167 |
167 |
167 |
167 |
167 |
167 |
167 |
167 |
|
Y |
89 |
81 |
85 |
85 |
85 |
86 |
88 |
88 |
89 |
89 |
89 |
90 |
|
X |
167 |
167 |
167 |
168 |
168 |
168 |
168 |
168 |
168 |
168 |
168 |
168 |
|
Y |
91 |
91 |
92 |
81 |
82 |
83 |
87 |
88 |
88 |
90 |
92 |
93 |
|
X |
168 |
169 |
169 |
169 |
169 |
169 |
169 |
169 |
169 |
169 |
169 |
169 |
|
Y |
93 |
79 |
83 |
87 |
87 |
87 |
88 |
88 |
89 |
91 |
91 |
91 |
|
X |
169 |
169 |
169 |
169 |
170 |
170 |
170 |
170 |
170 |
170 |
170 |
170 |
|
Y |
91 |
91 |
92 |
92 |
81 |
86 |
88 |
88 |
90 |
90 |
90 |
90 |
|
X |
170 |
170 |
170 |
170 |
170 |
170 |
170 |
171 |
171 |
171 |
171 |
171 |
|
Y |
91 |
91 |
91 |
92 |
93 |
95 |
96 |
83 |
85 |
89 |
89 |
90 |
|
X |
171 |
171 |
171 |
171 |
171 |
171 |
172 |
172 |
172 |
172 |
172 |
172 |
|
Y |
91 |
91 |
91 |
92 |
94 |
97 |
82 |
87 |
88 |
89 |
90 |
91 |
|
X |
172 |
172 |
172 |
172 |
172 |
172 |
173 |
173 |
173 |
173 |
173 |
173 |
|
Y |
91 |
94 |
96 |
98 |
99 |
99 |
84 |
87 |
89 |
89 |
90 |
90 |
|
X |
173 |
173 |
173 |
174 |
174 |
174 |
174 |
174 |
174 |
175 |
175 |
175 |
|
Y |
90 |
91 |
96 |
86 |
88 |
90 |
91 |
96 |
97 |
85 |
89 |
90 |
Окончание таблицы 3
|
X |
175 |
175 |
175 |
176 |
176 |
176 |
176 |
176 |
176 |
176 |
176 |
176 |
|
Y |
90 |
91 |
95 |
82 |
86 |
87 |
88 |
90 |
92 |
93 |
93 |
93 |
|
X |
176 |
177 |
178 |
178 |
178 |
178 |
179 |
179 |
179 |
180 |
180 |
180 |
|
Y |
95 |
87 |
89 |
90 |
90 |
91 |
85 |
85 |
99 |
85 |
90 |
98 |
|
X |
181 |
181 |
182 |
183 |
184 |
185 |
186 |
187 |
190 |
|
Y |
89 |
92 |
90 |
90 |
98 |
91 |
92 |
86 |
105 |
Cоставим новую таблицу, в которой отразим частоты появления случайных величин ![]() и относительные частоты
и относительные частоты ![]() .
.
Таблица 4
Дискретный вариационный ряд
|
I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
148 |
155 |
156 |
157 |
158 |
159 |
160 |
161 |
162 |
163 |
164 |
165 |
|
|
1 |
1 |
2 |
2 |
1 |
3 |
3 |
6 |
6 |
9 |
15 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
166 |
167 |
168 |
169 |
170 |
171 |
172 |
173 |
174 |
175 |
176 |
177 |
|
|
8 |
14 |
10 |
15 |
15 |
11 |
12 |
9 |
6 |
6 |
10 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
|
|
178 |
179 |
180 |
181 |
182 |
183 |
184 |
185 |
186 |
187 |
190 |
|
|
4 |
3 |
3 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
В данном примере случайные величины сплошь заполняют промежуток (148;190). Число возможных значений велико. Их нельзя представить в виде случайных величин, принимающих отдельные, изолированные значения, тем самым отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины. Поэтому для построения вариационного ряда будем использовать интервальный ряд распределения. Весь возможный интервал варьирования разобьём на конечное число интервалов и подсчитаем частоту попадания значений величины в каждый интервал. Минимальное и максимальное значения случайной величины: ![]() Тогда интервал варьирования R («размах») будет равен R=
Тогда интервал варьирования R («размах») будет равен R=![]() Длину интервала рассчитывают по формуле:
Длину интервала рассчитывают по формуле:
 (6)
(6)
При этом значение признака, находящегося на границе интервалов относят к правой границе интервала.
На практике считают, что правильно составленный ряд распределения содержит от 6 до 15 частичных интервалов. Часто интервальный вариационный ряд заменяют дискретным вариационным рядом, выбирая средние значения интервала (таблица №7).
Для данного примера 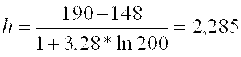 , округлим до 3, т. е. размер интервала H=3, а число интервалов будет равно 14. Соответствующий интервальный вариационный ряд приведён в таблице №5.
, округлим до 3, т. е. размер интервала H=3, а число интервалов будет равно 14. Соответствующий интервальный вариационный ряд приведён в таблице №5.
Таблица 5
Интервальный вариационный ряд
|
Индекс интервала I |
Число покупателей (интервалы)
|
Частота
|
Относительная частота
|
|
1 |
148-151 |
1 |
1/200 |
|
2 |
151-154 |
0 |
0 |
|
3 |
154-157 |
5 |
5/200 |
|
4 |
157-160 |
7 |
7/200 |
|
5 |
160-163 |
21 |
21/200 |
|
6 |
163-166 |
38 |
38/200 |
|
7 |
166-169 |
39 |
39/200 |
|
8 |
169-172 |
38 |
38/200 |
|
9 |
172-175 |
21 |
21/200 |
|
10 |
175-178 |
15 |
15/200 |
|
Окончание таблицы 5 | |||
|
Индекс интервала I |
Число покупателей (интервалы)
|
Частота
|
Относительная частота
|
|
11 |
178-181 |
8 |
8/200 |
|
12 |
181-184 |
3 |
3/200 |
|
13 |
184-187 |
3 |
3/200 |
|
14 |
187-190 |
1 |
1/200 |
![]() =1
=1
2) После составления вариационного ряда необходимо построить функцию распределения выборки или эмпирическую функцию F*(X)=![]() , то есть функцию найденную опытным путём. Здесь
, то есть функцию найденную опытным путём. Здесь ![]() – относительная частота события Х< х, n - общее число значений.
– относительная частота события Х< х, n - общее число значений.
Эмпирическое распределение можно изобразить в виде полигона, гистограммы или ступенчатой кривой.
![]() Построим выборочную функцию распределения. Очевидно, что для
Построим выборочную функцию распределения. Очевидно, что для ![]() функция
функция ![]() так как
так как ![]() . На концах интервалов значения функции
. На концах интервалов значения функции ![]() рассчитаем в виде «нарастающей относительной частоты» (Таблица 6).
рассчитаем в виде «нарастающей относительной частоты» (Таблица 6).
Таблица 6
Расчёт эмпирической функции распределения
|
Индекс интервала I |
|
|
1 |
1/200 |
|
2 |
1/200 |
|
3 |
1/200+5/200=6/200 |
|
4 |
6/200+7/200=13/200 |
|
5 |
13/200+21/200=34/200 |
|
6 |
34/200+38/200=72/200 |
|
Окончание таблицы 6 | |
|
Индекс интервала I |
|
|
7 |
72/200+39/200=111/200 |
|
8 |
111/200+38/200=149/200 |
|
9 |
149/200+21/200=170/200 |
|
10 |
170/200+15/200=185/200 |
|
11 |
185/200+8/200=193/200 |
|
12 |
193/200+3/200=196/200 |
|
13 |
196/200+3/200=199/200 |
|
14 |
199/200+1/200=200/200 |
Табличные значения не полностью определяют выборочную функцию распределения непрерывной случайной величины, поэтому при графическом изображении её доопределяют, соединив точки графика, соответствующие концам интервала, отрезками прямой (рис.1).
Полученные данные, представленные в виде вариационного ряда, изобразим графически в виде ломаной линии (полигона), связывающей на плоскости точки с координатами ![]() , где
, где ![]() - среднее значение интервала
- среднее значение интервала ![]() , а
, а ![]() - относительная частота.(таблица 7 и рис.2). На этом же рисунке отобразим пунктирной линией выравнивающие (теоретические) частоты.
- относительная частота.(таблица 7 и рис.2). На этом же рисунке отобразим пунктирной линией выравнивающие (теоретические) частоты.
Таблица 7
Дискретный вариационный ряд
|
Номер интервала I |
Среднее значение интервала
|
Относительная частота
|
Выборочная Оценка плотности вероятности
|
|
1 |
149,5 |
0,005 |
0,002 |
|
2 |
152,5 |
0 |
0 |
|
3 |
155,5 |
0,025 |
0,008 |
|
Окончание таблицы 7 | |||
|
4 |
158,5 |
0,035 |
0,012 |
|
5 |
161,5 |
0,105 |
0,035 |
|
6 |
164,5 |
0,19 |
0,063 |
|
7 |
167,5 |
0,195 |
0,065 |
|
8 |
170,5 |
0,19 |
0,063 |
|
9 |
173,5 |
0,105 |
0,035 |
|
10 |
176,5 |
0,075 |
0,025 |
|
11 |
179,5 |
0,04 |
0,013 |
|
12 |
182,5 |
0,015 |
0,005 |
|
13 |
185,5 |
0,015 |
0,005 |
|
14 |
188,5 |
0,005 |
0,002 |
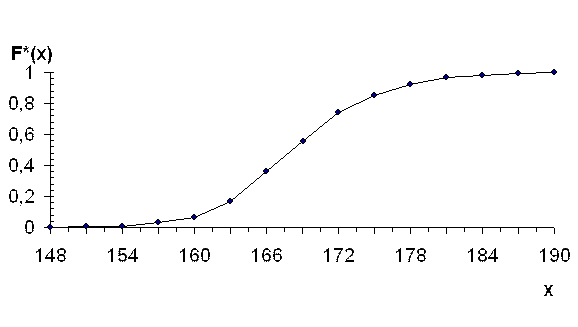 |
Рис.1
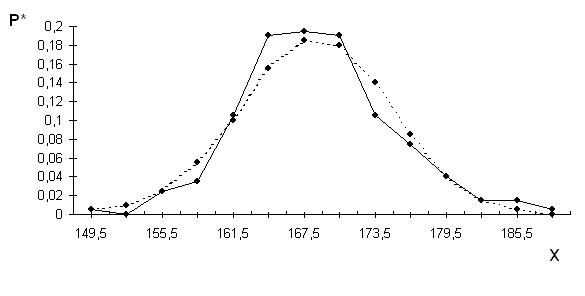 |
Рис.2
На основании полученных выборочных данных необходимо сделать предположение, что изучаемая величина распределена по некоторому определённому закону. Для того чтобы проверить, согласуется ли это предположение с данными наблюдений, вычисляют частоты полученных в наблюдениях значений, т. е. находят теоретически сколько раз величина Х должна была принять каждое из наблюдавшихся значений, если она распределена по предполагаемому закону. Для этого находят выравнивающие (теоретические) частоты по формуле:
![]() (7)
(7)
Где N – число испытаний,
![]() - вероятность наблюдаемого значения
- вероятность наблюдаемого значения ![]() , вычисленная при допущении, что Х имеет предполагаемое распределение.
, вычисленная при допущении, что Х имеет предполагаемое распределение.
Эмпирические (полученные из таблицы) и выравнивающие частоты сравнивают, и при небольшом расхождении данных делают заключение о выбранном законе распределения.
Предположим, что случайная величина Х распределена нормально (см. комментарии к задаче № 4). В этом случае выравнивающие частоты находят по формуле:
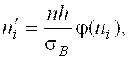 (8)
(8)
Где N-число испытаний,
H-длина частичного интервала,
![]() -выборочное среднее квадратичное отклонение,
-выборочное среднее квадратичное отклонение,
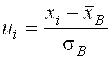 (
(![]() - середина I – го частичного интервала)
- середина I – го частичного интервала)
 – функция Лапласа (9)
– функция Лапласа (9)
Результаты вычислений отобразим в таблице №8.
Сравнение графиков (рис.2) наглядно показывает близость выравнивающих частот к наблюдавшимся и подтверждает правильность допущения о том, что обследуемый признак распределён нормально.
Таблица 8
Расчёт выравнивающих частот
|
|
|
|
|
|
|
|
|
149,5 152,5 155,5 158,5 161,5 164,5 167,5 170,5 173,5 176,5 179,5 182,5 185,5 188,5 |
-19,5 -16,5 -13,5 -10,5 -7,05 -4,05 -1,05 1,95 4,95 7,95 10,95 13,95 16,95 19,95 |
-3 -2,53 -2,06 -1,59 -1,11 -0,64 -0,17 0,31 0,78 1,25 1,73 2,2 2,67 3,15 |
0,004 0,02 0,048 0,11 0,22 0,33 0,396 0,38 0,3 0,18 0,09 0,04 0,011 0,003 |
0,42 1,55 4,54 10,68 20,37 31,0 37,48 36,0 28,0 17,34 8,44 3,37 1,06 0,26 |
1 2 5 11 20 31 37 36 28 17 8 3 1 0 |
0,05 0,01 0,025 0,055 0,1 0,155 0,185 0,18 0,14 0,085 0,04 0,015 0,005 0 |
![]()
Интервальный вариационный ряд графически изобразим в виде гистограммы (рис.3). На оси Х отложим интервалы длиной H=3, а на оси Y значения ![]() ,расчёт которых представлен в таблице №7. Площадь под гистограммой равна сумме всех относительных частот, т. е. единице.
,расчёт которых представлен в таблице №7. Площадь под гистограммой равна сумме всех относительных частот, т. е. единице.
Графическое изображение вариационных рядов в виде полигона и гистограммы позволяет получать первоначальное представление о закономерностях, имеющих место в совокупности наблюдений.
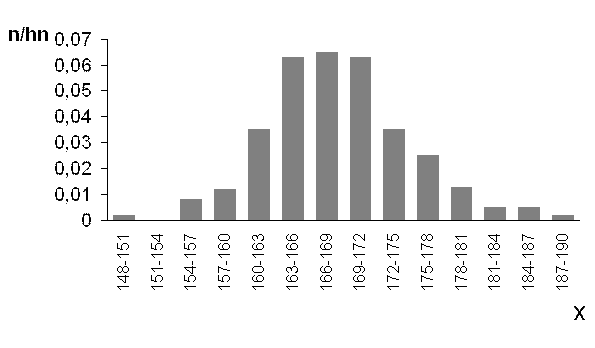
Рис.3![]()
3) Найдём числовые характеристики вариационного ряда, используя таблицу №4.
Выборочная средняя (![]() ):
):
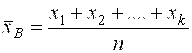
или 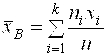 , (10)
, (10)
Где ![]() - частоты,
- частоты,
А ![]() -объём выборки. Выборочная средняя является оценкой математического ожидания (среднего значения теоретического закона распределения).
-объём выборки. Выборочная средняя является оценкой математического ожидания (среднего значения теоретического закона распределения).
В некоторых случаях ![]() удобнее рассчитать с помощью условных вариант. В нашем случае варианты
удобнее рассчитать с помощью условных вариант. В нашем случае варианты ![]() - большие числа, поэтому используем разность:
- большие числа, поэтому используем разность:
![]() (11)
(11)
Где С – произвольно выбранное число (ложный нуль). В этом случае
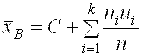 . (12)
. (12)
Для изменения значения варианты можно ввести также условные варианты путём использования масштабного множителя:
![]() , (13)
, (13)
Где ![]() (B выбирается положительным или отрицательным числом).
(B выбирается положительным или отрицательным числом).
![]()
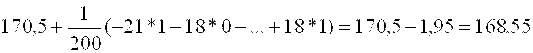 . Здесь С – середина 8-го интервала.
. Здесь С – середина 8-го интервала.
Выборочная дисперсия (![]() ):
):
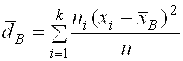 (14)
(14)
![]() также может быть рассчитана с помощью условных вариант:
также может быть рассчитана с помощью условных вариант:
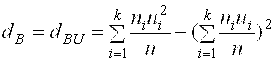 (15)
(15)
![]() =
=![]() (1*441+0*324+…+1*324)- 1,95²=40,21
(1*441+0*324+…+1*324)- 1,95²=40,21
Среднеквадратическое отклонение:
![]() =
=![]() (16)
(16)
![]() =
=![]() =6,34
=6,34
Найдем несмещённую оценку дисперсии и среднеквадратического отклонения («исправленную» выборочную дисперсию и среднеквадратическое отклонение) по формулам:
![]()
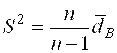 и
и  (17)
(17)
![]() =
=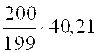 =40,41 и S=
=40,41 и S=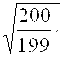 6,34=6,36
6,34=6,36
Доверительный интервал для оценки математического ожидания с надёжностью ![]() 0,95 определяют по формуле:
0,95 определяют по формуле:
P(![]() -T
-T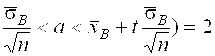 Ф(t)=
Ф(t)=![]() (18)
(18)
Из соотношения Ф(Z)=![]() /2 вычисляют значение функции Лапласа: Ф(Z)=0,475. По таблице значений функции Лапласа ( Приложение А) находят Z=1,96. Таким образом,
/2 вычисляют значение функции Лапласа: Ф(Z)=0,475. По таблице значений функции Лапласа ( Приложение А) находят Z=1,96. Таким образом,
168,55-1,96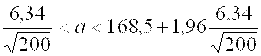 ,
,
167,67<A<169,43.
Доверительный интервал для оценки среднего квадратичного отклонения случайной величины находят по формуле:
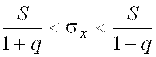 , (19)
, (19)
Где S – несмещённое значение выборочного среднего квадратичного отклонения;
Q – параметр, который находится по таблице (Приложение В) на основе известного объёма выборки n и заданной надёжности оценки ![]() .
.
На основании данных значений ![]() =0,95 и N=200 по таблице (Приложение В) можно найти значение Q=0,099. Таким образом,
=0,95 и N=200 по таблице (Приложение В) можно найти значение Q=0,099. Таким образом,
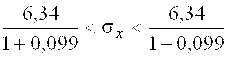 ,
,
5,79<![]()
V=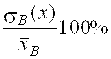 (20)
(20)
4) Проведём статистическую проверку гипотезы о нормальном распределении. Нормальный закон распределения имеет два параметра (R=2): математическое ожидание и среднее квадратическое отклонение. По выборочным данным (таблицы 5 и 7) полученные оценки параметров нормального распределения, вычисленные выше:
![]()
![]() ,
, 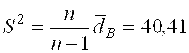 , S=6,36.
, S=6,36.
Для расчёта теоретических частот ![]() используют табличные значения функции Лапласа Ф(Z). Алгоритм вычисления
используют табличные значения функции Лапласа Ф(Z). Алгоритм вычисления ![]() состоит в следующем:
состоит в следующем:
- по нормированным значениям случайной величины Z находят значения Ф(Z), а затем ![]() :
:
 ,
, ![]() =0,5+Ф(
=0,5+Ф(![]() ).
).
Например,
![]() ;
; 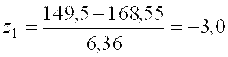 ; Ф(-3,0)=-0,4987;
; Ф(-3,0)=-0,4987;
![]() ;
;
- далее вычисляют вероятности ![]() =P(
=P(![]() ;
;
- находят числа ![]() , и если некоторое
, и если некоторое ![]() <5, то соответствующие группы объединяются с соседними.
<5, то соответствующие группы объединяются с соседними.
Результаты вычисления ![]() ,
, ![]() , и
, и ![]() приведены в таблице 9.
приведены в таблице 9.
По формуле
![]() =
= (21)
(21)
можно сделать проверку расчетов.

По таблице (приложения Г) можно найти число ![]() по схеме: для уровня значимости α=0,05 и числа степеней свободы L=K-R-1=9-2-1=6
по схеме: для уровня значимости α=0,05 и числа степеней свободы L=K-R-1=9-2-1=6![]()
![]() =12,6. Следовательно, критическая область - (12,6;
=12,6. Следовательно, критическая область - (12,6;![]() ). Величина
). Величина ![]() =15,61 входит в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, отвергается.
=15,61 входит в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, отвергается.
При α=0,1 ![]() =10,6. Критическая область - (10,6;
=10,6. Критическая область - (10,6;![]() ). Величина
). Величина ![]() =15,61 также входит в критическую область и гипотеза о нормальном законе распределения величины Х отвергается.
=15,61 также входит в критическую область и гипотеза о нормальном законе распределения величины Х отвергается.
При α=0,01 ![]() =16,8, (16,8;
=16,8, (16,8;![]() ). В этом случае нет оснований отвергать гипотезу о нормальном законе распределения.
). В этом случае нет оснований отвергать гипотезу о нормальном законе распределения.
Таблица 9
Определение ![]()
|
I |
|
|
Ф( |
|
|
|
|
|
|
0 |
149,5 |
0 |
-0,500 |
0,000 |
0,0013 |
0,0013 |
0,26 |
- |
|
1 |
149,5 152,5 |
1 |
-0,449 |
0,0013 |
0,0059 |
0,0046 |
0,92 |
- |
|
2 |
152,5 155,5 |
0 |
-0,494 |
0,0059 |
0,02 |
0,014 |
2,8 |
- |
|
3 |
155,5 158,5 |
5 |
-0,48 |
0,02 |
0,057 |
0,037 |
7,4 |
2,54 |
|
4 |
158,5 161,5 |
7 |
-0,44 |
0,057 |
0,134 |
0,077 |
15,4 |
4,58 |
|
5 |
161,5 164,5 |
21 |
-0,37 |
0,134 |
0,26 |
0,126 |
25,2 |
0,7 |
|
6 |
164,5 167,5 |
38 |
-0,24 |
0,26 |
0,433 |
0,1725 |
34,5 |
0,36 |
|
7 |
167,5 170,5 |
39 |
-0,07 |
0,433 |
0,62 |
0,188 |
37,6 |
0,06 |
|
8 |
170,5 173,5 |
38 |
0,12 |
0,62 |
0,78 |
0,16 |
32 |
1,125 |
|
9 |
173,5 176,5 |
21 |
0,28 |
0,78 |
0,89 |
0,11 |
22 |
0,045 |
|
10 |
176,5 179,5 |
15 |
0,39 |
0,89 |
0,96 |
0,07 |
14 |
0,071 |
|
11 |
179,5 182,5 |
8 |
0,46 |
0,96 |
0,99 |
0,03 |
6 |
6,125 |
|
12 |
182,5 185,5 |
3 |
0,49 |
0,99 |
0,996 |
0,006 |
1,2 |
- |
|
13 |
185,5 188,5 |
3 |
0,496 |
0,996 |
0,999 |
0,003 |
0,6 |
- |
|
14 |
188,5
|
1 |
0,5 |
0,999 |
1,0 |
0,001 |
0,2 |
- |
![]()
![]() ,0000
,0000 ![]()
2 часть
1) Данные таблицы 3 сгруппируем в корреляционную таблицу 10.
2) Строим в системе координат множество, состоящее из 200 экспериментальных точек (рисунок 4).
По расположению точек делаем заключение о том, что экономико-математическую модель можно искать в виде ![]() .
.
3) Найдём выборочные уравнения линейной регрессии.
Для упрощения расчётов разобьём случайные величины на интервалы и выберем средние значения. Для величины Х указанные действия были выполнены в 1 части задания.
Таблица 10
Корреляционная таблица
|
|
105 |
100 |
99 |
98 |
97 |
96 |
95 |
94 |
93 |
92 |
91 |
90 |
89 |
88 |
87 |
86 |
85 |
84 |
83 |
82 |
81 |
80 |
79 |
Y/X |
|
1 |
1 |
148 | ||||||||||||||||||||||
|
1 |
1 |
155 | ||||||||||||||||||||||
|
2 |
1 |
1 |
156 | |||||||||||||||||||||
|
2 |
1 |
1 |
157 | |||||||||||||||||||||
|
1 |
1 |
158 | ||||||||||||||||||||||
|
3 |
1 |
1 |
1 |
159 | ||||||||||||||||||||
|
3 |
1 |
1 |
1 |
160 | ||||||||||||||||||||
|
6 |
1 |
1 |
2 |
1 |
1 |
161 | ||||||||||||||||||
|
6 |
1 |
1 |
1 |
1 |
1 |
1 |
162 | |||||||||||||||||
|
9 |
1 |
1 |
2 |
1 |
3 |
1 |
163 | |||||||||||||||||
|
15 |
1 |
2 |
2 |
3 |
1 |
1 |
1 |
3 |
2 |
164 | ||||||||||||||
|
15 |
4 |
1 |
2 |
1 |
4 |
1 |
1 |
165 | ||||||||||||||||
|
8 |
2 |
1 |
1 |
3 |
1 |
166 | ||||||||||||||||||
|
14 |
1 |
2 |
1 |
3 |
2 |
1 |
3 |
1 |
167 | |||||||||||||||
|
10 |
2 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
168 | |||||||||||||||
|
15 |
2 |
5 |
1 |
2 |
3 |
1 |
1 |
169 | ||||||||||||||||
|
15 |
1 |
1 |
1 |
1 |
3 |
4 |
2 |
1 |
1 |
170 | ||||||||||||||
|
Продолжение таблицы 10 | ||||||||||||||||||||||||
|
11 |
1 |
1 |
1 |
3 |
1 |
2 |
1 |
1 |
171 | |||||||||||||||
|
12 |
2 |
1 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
172 | |||||||||||||
|
9 |
1 |
1 |
3 |
2 |
1 |
1 |
173 | |||||||||||||||||
|
6 |
1 |
1 |
1 |
1 |
1 |
1 |
174 | |||||||||||||||||
|
6 |
1 |
1 |
2 |
1 |
1 |
175 | ||||||||||||||||||
|
10 |
1 |
3 |
1 |
1 |
1 |
1 |
1 |
1 |
176 | |||||||||||||||
|
1 |
1 |
177 | ||||||||||||||||||||||
|
4 |
1 |
2 |
1 |
178 | ||||||||||||||||||||
|
3 |
1 |
2 |
179 | |||||||||||||||||||||
|
3 |
1 |
1 |
1 |
180 | ||||||||||||||||||||
|
2 |
1 |
1 |
181 | |||||||||||||||||||||
|
1 |
1 |
182 | ||||||||||||||||||||||
|
1 |
1 |
183 | ||||||||||||||||||||||
|
1 |
1 |
184 | ||||||||||||||||||||||
|
1 |
1 |
185 | ||||||||||||||||||||||
|
1 |
1 |
1 |
186 | |||||||||||||||||||||
|
1 |
187 | |||||||||||||||||||||||
|
1 |
1 |
190 | ||||||||||||||||||||||
|
200 |
1 |
1 |
3 |
3 |
3 |
4 |
3 |
7 |
8 |
11 |
28 |
24 |
19 |
18 |
17 |
7 |
12 |
10 |
7 |
6 |
4 |
2 |
2 |
|
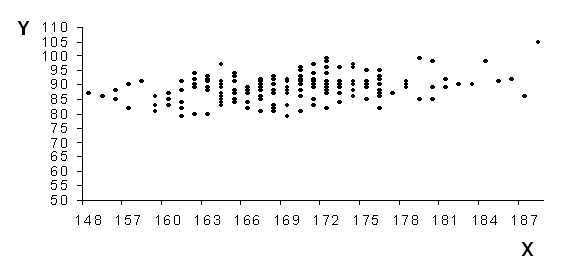 |
Рис.4
Для случайной величины Y, используя (1), получим H=2, число интервалов равно 13. Результаты внесём в таблицу со сгруппированными данными №11.
Находим средние значения ![]() , по формулам:
, по формулам:
 , (22)
, (22)
 , (23)
, (23)
 , (24)
, (24)
 . (25)
. (25)
![]()
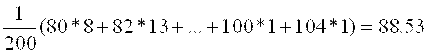
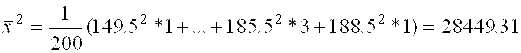
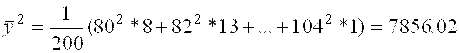
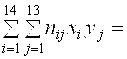 149,5*86+155,5(82+…+90)+…+188,5*104=2986101
149,5*86+155,5(82+…+90)+…+188,5*104=2986101
Используя формулы:
![]() , (26)
, (26)
![]() , (27)
, (27)
Получим
![]() =
=![]() ,
,![]() =
=![]()
Таблица 11
Сгруппированные данные выборки
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 | ||
|
XY |
149,5 |
152,5 |
155,5 |
158,5 |
161,5 |
164,5 |
167,5170,5173,5 |
170,5 |
173,5 |
176,5 |
179,5 |
182,5 |
185,5 |
188,5 |
| |
|
1 |
80 |
1 |
3 |
3 |
1 |
8 | ||||||||||
|
2 |
82 |
1 |
2 |
1 |
3 |
3 |
2 |
1 |
13 | |||||||
|
3 |
84 |
1 |
1 |
2 |
9 |
3 |
1 |
2 |
3 |
22 | ||||||
|
4 |
86 |
1 |
1 |
2 |
7 |
5 |
1 |
1 |
3 |
1 |
24 | |||||
|
5 |
88 |
1 |
6 |
7 |
10 |
6 |
4 |
2 |
1 |
37 | ||||||
|
6 |
90 |
1 |
1 |
4 |
6 |
9 |
14 |
9 |
4 |
1 |
2 |
1 |
52 | |||
|
7 |
92 |
3 |
1 |
6 |
3 |
4 |
1 |
1 |
19 | |||||||
|
8 |
94 |
1 |
4 |
3 |
1 |
1 |
10 | |||||||||
|
9 |
96 |
1 |
3 |
3 |
7 | |||||||||||
|
10 |
98 |
3 |
2 |
1 |
6 | |||||||||||
|
11 |
100 |
1 |
1 | |||||||||||||
|
12 |
102 | |||||||||||||||
|
13 |
104 |
1 |
1 | |||||||||||||
|
|
1 |
5 |
7 |
21 |
38 |
39 |
38 |
21 |
15 |
8 |
3 |
3 |
1 |
200 |
4) Вычисляем выборочный коэффициент корреляции ![]() по формуле:
по формуле:
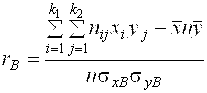 . (28)
. (28)
![]() =
=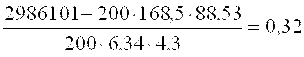
Принято считать, что если 0,1<![]() <0,3 – связь слабая, если 0,3<
<0,3 – связь слабая, если 0,3<![]() <0,5 – связь умеренная, если 0,5<
<0,5 – связь умеренная, если 0,5<![]() <0,7 – связь заметная, если 0,7<
<0,7 – связь заметная, если 0,7<![]() <0,9 – связь высокая, если 0,9<
<0,9 – связь высокая, если 0,9<![]() <0,99 – связь весьма высокая.
<0,99 – связь весьма высокая.
Для данного примера связь между X и Y умеренная.
Затем получают выборочное уравнение линейной регрессии Y на X в виде:
 (29)
(29)
И выборочное уравнение линейной регрессии X на Y :
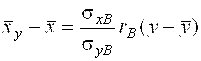 . (30)
. (30)
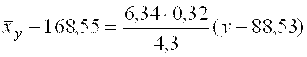 и
и
![]()
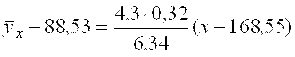 или
или
![]()
Вычисления сумм рекомендуем проводить с помощью пакетов прикладных математических программ (сегодня их существует много).
| < Предыдущая | Следующая > |
|---|