0. Предисловие
Пособие написано на основании курса, прочитанного авторами студентам Тверского института экологии и права. Мы исходили из того, что курс математики для юристов должен, с одной стороны, быть достаточно широким, чтобы играть развивающую, гуманитарную роль. С другой стороны, он должен быть и достаточно содержательным, чтобы студенты научились решать хотя бы несложные прикладные задачи.
Курс рассчитан всего на 24—26 часов, поэтому по содержанию может быть только продолжением на более высоком уровне школьного курса математики. Небольшой объем не позволил нам рассказать о других разделах математики, с которыми, на наш взгляд, было бы также полезно познакомиться будущему юристу. О них можно прочитать в книгах, список которых приведен на с. 222-223.
Изложение теории сопровождается упражнениями и типовыми заданиями. Последние служат основанием для индивидуальных домашних заданий. За каждое индивидуальное задание студент получает определенное число баллов. Общее число баллов (рейтинг) является основанием для получения (или не получения) зачета. Студентам могут быть предложены также курсовые работы по истории математики, по отдельным разделам математики — арифметике, комбинаторике, элементарной статистике.
Предлагаемый курс служит введением в более серьезную математику. Если учащийся захочет более детально разобраться в каком-либо разделе или какой-либо задаче (индивидуально, в рамках специального курса или факультатива), он сможет, освоив это пособие, обратиться к специальной литературе.
Авторы глубоко признательны рецензентам Н. С. Шерстневой и А. В. Гладкому, а также своим коллегам О. М. Виноградову, А. И. Катулеву, И. Ш. Могилевскому и Г. С. Шарову, прочитавшим рукопись и сделавшим много полезных замечаний. Особую благодарность мы выражаем руководству Тверского института экологии и права и инженеру-программисту Н. Л. Ивановой, без помощи которых эта книга навряд ли была бы издана в этом тысячелетии.
Я. Б. Тихомиров, А. М. Шелехов
Введение: Нужна ли юристу математика?
Авторы этого пособия полагают, что нужна. Математика — это часть общечеловеческой культуры, такая же неотъемлемая и важная, как право, медицина, естествознание и многое другое. Все наилучшие достижения человеческой мысли и составляют основу гуманитарного образования, необходимого каждому современному человеку. Таким образом, для студента гуманитария математика прежде всего Общеобразовательная дисциплина, Как, например, право для студента математика.
Но для юриста значение математики этим не исчерпывается. В юриспруденции, как и в математике, применяются одни и те же методы рассуждений, цель которых — выявить истину. Любой правовед, как и математик, должен уметь рассуждать логически, уметь применять на практике индуктивный и дедуктивный методы (вспомните Шерлока Холмса!). Поэтому, Занимаясь математикой, будущий правовед формирует свое профессиональное мышление.
Наконец, применение математических методов расширяет возможности каждого специалиста. В юридической практике важную роль играет статистика, умение правильно обработать информацию, сделать достоверный вывод или прогноз на основании имеющегося статистического материала. Ценность специалиста существенно возрастает, если он умеет делать все это.
Настоящее пособие помогает достичь указанных целей. Но написать его оказалось делом весьма непростым. Прежде всего потому, что предполагается обучать математике тех, кто уже мысленно с ней распрощался после окончания школы и полагал, что больше с ней не встретится. Понимая все это, мы начинаем наш курс с повторения школьного материала, несколько его обобщая и углубляя. Мы предлагаем учащимся такие разделы математики и такую последовательность изложения, при которых, на наш взгляд, усвоение будет происходить наиболее просто и естественно. В этом смысле изложение не является строгим и поэтому наше пособие отличается от стандартного математического курса примерно так же, как сборник рассказов от романа. Мы обсуждаем важнейшие математические понятия: число, вектор, функция, предел, аксиома, вероятность и показываем, как развивались математические идеи, заключенные в этих понятиях. Основная содержательная часть пособия представляет собой элементарное введение в курс теории вероятностей и математической статистики. Предполагается, что именно этому материалу будет посвящена большая часть практических занятий.
1.1. Натуральные, целые и рациональные числа
Известные нам числа 1, 2, 3... называются Натуральными. Их используют для счета или обозначения Количества предметов, например: один юрист, два юриста и т. д. Кроме того, с помощью натуральных чисел обозначают Порядок предметов. Например, если всех милиционеров в отделении выстроить по росту, то каждому из них можно присвоить номер: первый милиционер, второй милиционер и т. д. Поэтому различают Количественные числа — один, два, три, четыре..., и Порядковые числа — первый, второй, третий...
Чтобы записывать натуральные числа, большие десяти, мы пользуемся так называемой Десятичной позиционной системой. Слово «позиционная» означает, что значение цифры зависит от ее места, например:
147 = 1 • 100 + 4 • 10 + 7 • 1,
714 = 7 • 100 + 1 • 10 + 4 • 1,
471 = 4 • 100 + 7 • 10 + 1 • 1.
Слово «десятичная» означает, что используются степени десятки. В другой системе, например, пятиричной, содержащей всего пять цифр 0, 1, 2, 3, 4, числовая позиционная запись расшифровывается так:
143 = 1 • 52 + 4 • 5 + 3 • 1;
В двоичной системе, содержащей всего две цифры 0 и 1, мы получим:
1 011 001 = 1 • 26 + 0 • 25 + 1 • 24 + 1 • 23 + 0•22 + 0•2 + 1•1.
Натуральные числа можно, как известно, складывать, вычитать, умножать и делить. Однако эти операции неравноценны. Очевидно, что сумма А + B любых двух натуральных чисел А и B снова будет натуральным числом; то же самое можно сказать и о произведении Ab. При этом порядок слагаемых и сомножителей не играет роли, т. е. А + B = B+а И аB = Bа.
Что же касается операций вычитания и деления, то здесь ситуация иная. Например, разность 5 – 2 = 3 — число натуральное, но натурального числа 2 – 5 не существует. В последнем случае используют так называемые Отрицательные числа и записывают 2 – 5 = –3, 4 – 10 = –6 и т. п. Числа А И –а называются Противоположными.
Между натуральными числами и целыми отрицательными числами находится число 0 (нуль). Его рассматривают как количественное число; нуль предметов данного вида (например, попугаев в Антарктиде) означает отсутствие предметов данного вида. Пользуясь математической терминологией, можно сказать, что множество попугаев, проживающих в Антарктиде, есть Пустое множество.* Нуль обладает следующими свойствами:
1) а + 0 = А;
2) А + (–А) = 0;
3) на нуль делить нельзя.
* Понятие множества обсуждается в гл. VIII.
Натуральные числа, целые отрицательные числа и число нуль называются в совокупности Целыми числами. Множество всех натуральных чисел обозначается символом N, множество всех целых чисел — символом Z. Наглядно целые числа представляют точками на прямой (шкала термометра):
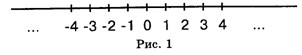
В отличие от множества натуральных чисел, множество целых чисел устроено более «демократично»: любые два целых числа можно вычитать друг из друга и результат вычитания всегда будет также целым числом. Математики говорят, что множество целых чисел Замкнуто относительно операций сложения и вычитания, И что это множество получено Расширением множества натуральных чисел.
Потребность расширить множество натуральных чисел возникает и при делении. Например, семь милиционеров нельзя разделить на четыре равные части — такого количества милиционеров 7/4 не существует. Но мы вполне можем разделить семь миллионов рублей на четыре равные части. Это число (1 миллион 750 тысяч) составляет 7/4 от общей суммы. Аналогичный смысл имеет обозначение ![]() , где А и B — любые натуральные или даже целые числа (B ¹ 0). Числа вида
, где А и B — любые натуральные или даже целые числа (B ¹ 0). Числа вида ![]() называются Обыкновенными дробями или Рациональными числами.* Множество всех рациональных чисел обозначается символом Q.
называются Обыкновенными дробями или Рациональными числами.* Множество всех рациональных чисел обозначается символом Q.
* Между этими двумя понятиями есть некоторое различие. Например, одно и то же число 2/3 можно записать в виде различных дробей: 4/6, 6/9, 10/15 и т. д. Последние можно сократить, но дробь 2/3 сократить нельзя. Она является Несократимой.
Целое число А можно записать как дробь А/1, поэтому целые числа входят как часть во множество рациональных чисел. В этом случае говорят, что множество целых чисел является Подмножеством множества рациональных чисел. Точно так же, множество натуральных чисел является подмножеством множества целых чисел. Записывается это следующим образом:
![]()
А знак «![]() » читается так: «содержится в», «является подмножеством» или «является частью». Заметим, что во множестве рациональных чисел «равноправия» еще больше, чем во множестве целых чисел: любые два рациональных числа можно не только вычитать друг из друга, но можно и делить одно на другое (кроме деления на нуль!); при этом в результате указанных действий всегда будут получаться снова рациональные числа. Таким образом, множество рациональных чисел замкнуто относительно всех четырех операций: сложения, вычитания, умножения и деления.
» читается так: «содержится в», «является подмножеством» или «является частью». Заметим, что во множестве рациональных чисел «равноправия» еще больше, чем во множестве целых чисел: любые два рациональных числа можно не только вычитать друг из друга, но можно и делить одно на другое (кроме деления на нуль!); при этом в результате указанных действий всегда будут получаться снова рациональные числа. Таким образом, множество рациональных чисел замкнуто относительно всех четырех операций: сложения, вычитания, умножения и деления.
Все натуральные числа, за исключением единицы, подразделяются на Простые и Составные. Натуральное число называется Составным, если оно представляет собой произведение двух натуральных чисел, не равных единице, например: 4=2 • 2, 39 = 3 • 13, 111 = 3 • 37. Если натуральное число нельзя представить в виде такого произведения, то оно называется Простым, например: 2, 3, 5, 7, 11.
Простые числа играют в математике особую роль. В их жизни много загадочного, и математики, стремясь разгадать эти тайны, открыли (и продолжают открывать до сих пор!) интереснейшие свойства простых чисел, придумали оригинальные математические методы исследования, которые применяются не только в теории чисел, но и в других разделах математики.
Древнегреческий математик Эратосфен предложил способ получения простых чисел, который называется решетом Эратосфена. Представим себе ряд натуральных чисел:
![]()
Отметим (кружком) простое число 2 и затем вычеркнем все четные числа (или, как говорят, числа, кратные двум). Согласно определению, вычеркнутые числа не являются простыми, так как делятся на два и их можно записать в виде 2K. Затем отметим простое число 3 и вычеркнем все числа, кратные трем: 3, 6, 9, 12 и т. д. Эти числа не простые, а составные, так как их можно записать в виде 3K. Часть этих чисел, а именно четные, уже вычеркнута (на рис. 2 они зачеркнуты два раза). Следующее наименьшее незачеркнутое число — 5, оно простое. Выделим его, а затем вычеркнем все числа, кратные пяти: 10, 15, 20 и т. д. В результате останутся незачеркнутыми только простые числа.
Заметим, что осуществить описанную процедуру Полностью практически невозможно, так как Множество натуральных чисел бесконечно. Но мы можем, пользуясь решетом Эратосфена, найти «вручную» все простые числа, например, в первой тысяче натуральных чисел. Современные компьютеры позволили отодвинуть эту границу до 1020. Принципиально, возможности ЭВМ здесь не ограничены.
УПРАЖНЕНИЯ
1. Найдите такое число Х, что для любого числа А выполняется равенство Ха = А.
2. Вспомните, что такое четные и нечетные числа. Назовите все четные простые числа.
3. Будет ли множество четных чисел замкнуто относительно операций сложения, вычитания и умножения?
4. Назовите наименьшее натуральное число.
5. Сравните дроби: ![]() и
и ![]() ;
; ![]() и
и ![]() ;
; ![]() и
и ![]() ;
; ![]() и
и ![]() .
.
6. Вспомните, что такое среднее арифметическое двух, трех или нескольких чисел. Найдите среднее арифметическое следующих чисел:
А) 1 и 2; б) –3 и 5; в) ![]() и
и ![]() ; г)
; г) ![]() и 3; д)
и 3; д) ![]() ,
, ![]() и
и ![]() ;
; ![]() ,
, ![]() и
и ![]() .
.
7. Покажите, что следующие числа являются простыми:
2 • 3 + 1; 2 • 3 • 5 + 1; 2 • 3 • 5 • 7 + 1; 2 • 3 • 5 • 7 • 11+1.
Попробуйте предсказать общий результат.
ТИПОВОЕ ЗАДАНИЕ
1. Выполните следующие арифметические действия:
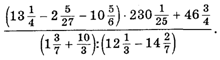
| Следующая > |
|---|