9.2. Извлечение из теории игр

Как мы уже отмечали, математические методы позволяют во многих ситуациях найти оптимальное реше­ние. Число таких математических методов довольно ве­лико, и многие из них весьма сложны. В этой книге мы продемонстрируем лишь некоторые из них, причем в самых простых ситуациях. Тем не менее, внимательный читатель, не имеющий предубеждения к математике, сможет почерпнуть много полезного и применить эти методы в своей работе.

Часто решения приходится принимать в конфликт­ной ситуации, когда сталкиваются интересы двух или более сторон, преследующих разные цели. Такие ситуа­ции возникают очень часто: военная сфера, конкурен­ция в экономике, спортивные состязания, судебная про­цедура и т. д. Математическая теория, анализирующая конфликтные ситуации, называется теорией игр. Игрой называется модель конфликтной ситуации. Покажем на простом примере, как строится и работает такая модель.

«Военная» игра

У нас имеется два вида вооружения — А1 (зенитки) и A2 (ракеты типа «земля-воздух»); у противника — два типа самолетов Б1 и Б2. Ход противника состоит в том, что он выбирает один из своих самолетов и посылает его бомбить нашу базу. Следовательно, у него 2 хода — Б1 и Б2. Наш ответный ход состоит в том, что мы выбираем один из видов вооружения и пытаемся сбить самолет. Следовательно, у нас тоже 2 хода — А1 и А2. Эту ситуа­цию можно смоделировать игрой 2´2, в которой 2 игро­ка — мы (игрок А) и противник (игрок Б). Прежде всего установим правила игры. Это означает, что нужно назна­чить Платежи, т. е. указать, сколько каждый игрок вы­игрывает или проигрывает, сделав тот или иной ход.* Обычно указывают выигрыши игрока А. Выигрышем может быть какая-то сумма денег, число баллов, вероят­ность попадания в цель и т. д. В нашем случае возьмем в качестве платежей вероятности поражения самолетов. Пусть оружие А1 поражает самолеты Б1 и Б2 с вероятно­стями 0,5 и 0,6, а оружие А2 — с вероятностями 0,6 и 0,7 соответственно. Составим Платежную матрицу, т. е. таб­лицу, в которой укажем выигрыши первого игрока:

* Мы рассматриваем так называемую антогонистическую игру, в которой проигрыш одного игрока равен выигрышу другого.

Главная идея теории игр состоит в том, что игрок А Считает своего противника не глупее себя, поэтому при каждом своем ходе он рассчитывает получить хотя бы наименьший выигрыш. Наименьший выигрыш при пер­вом ходе игрока А — это наименьшее число в первой строке матрицы, т. е. 0,5. Обозначим это число a1. Наи­меньший выигрыш игрока А при втором ходе будет a2 = 0,6, т. е. наименьшее число во второй строке пла­тежной матрицы. Но из двух ходов игрок А должен сде­лать тот, при котором его наименьший выигрыш будет больше, т. е. 0,6. Обозначим это число через a. В то же время второй игрок должен действовать так, чтобы его наибольший проигрыш был как можно меньше. Наи­больший проигрыш игрока Б при первом ходе будет bl = 0,6 (наибольшее число в первом столбце); при вто­ром ходе — b2 = 0,7 (наибольшее число во втором столб­це). Следовательно, игрок Б должен сделать первый ход, тогда его проигрыш будет не более b = 0,6. Запишем эти числа в таблицу:

Величина a называется Нижней ценой игры. или Максимином, величина b — Верхней ценой игры или Минимаксом. Итак, Оптимальная стратегия игрока А — сде­лать ход А2, А Оптимальная стратегия игрока Б — сде­лать ход Б1. В этом случае наименьший выигрыш игрока А будет максимальным — 0,6, а наибольший проигрыш игрока Б — минимальным, т. е. тоже 0,6. Легко прове­рить, что если один из игроков придерживается своей оптимальной стратегии, то и другому тоже невыгодно отклоняться от нее. В рассмотренной игре получилось так, что a = b. В этом случае говорят, что игра имеет Седловую точку в чистых стратегиях (у нас она 0,6). Как мы видим, в игре с седловой точкой оптимальные страте­гии игроков описываются весьма просто. При этом суще­ственно то, что при повторении игры при тех же услови­ях игроки должны делать те же самые ходы.

В следующем примере выбор оптимальной стратегии более сложен.

Игра «Поиск»

Дети играют в «преступника» и «милиционера». Игрок А прячется, Б ищет. Игрок А имеет два места, П1 и П2, где он может спрятаться. Игрок Б знает, где они находятся. Каждый из них может по своему усмотре­нию выбрать то или иное место (один — чтобы спря­таться, другой — чтобы найти). Таким образом, каждый игрок имеет по два хода.

Игрок А:

Первый ход (А1) — спрятаться в П1, второй ход (А2) — Спрятаться в П2.

Игрок Б:

Первый ход (Б1) — искать в П1, второй ход (Б2) — искать в П2.

Теперь назначим платежи. Если Б нашел А в первом или втором убежище, то А платит ему 1 руб., т. е. выиг­рыш игрока А равен –1. Если Б не находит А, то он платит игроку А 1 руб. Поэтому платежная матрица, со­стоящая из выигрышей игрока А, выглядит так:

Найдем как и выше, числа a и b. Получается следующая таблица:

Рассмотрим два принципиально разных случая.

1. Играют один раз. Тогда, поскольку a1 = a2 = a, Игроку А совершенно безразлично, какой шаг делать, А1 Или A2. В любом случае его минимальный выигрыш не меньше –1. То же самое можно сказать и о поведении игрока Б: как бы он не ходил, его максимальный про­игрыш не больше 1.

2. Игра повторяется многократно. Тогда игрок А не может делать все время один и тот же ход, иначе его противник разгадает стратегию и начнет выигрывать. Следовательно, игрок А должен чередовать свои ходы. Но если он будет чередовать их в каком-то определенном по­рядке, то противник через некоторое время разгадает его тактику и опять начнет выигрывать. Поэтому игрок А Должен вести себя как можно более непредсказуемо, т. е. выбирать каждый последующий ход каким-то случайным образом. Это можно делать с помощью монеты (орел-реш­ка) или игральной кости (чет-нечет).

В рассмотренной только что игре ходы каждого игрока имеют одинаковую цену, т. е. равноправны. Следо­вательно, нет никаких оснований предпочесть один ход (например, A1) другому (А2). Именно поэтому игрок оп­ределяет свою стратегию с помощью монеты или иг­ральной кости.

Следующая игра показывает, как выбрать стратегию в еще более сложной ситуации.

Игра «Коммерсант»

Коммерсант торгует темными очками и зонтиками, поэтому его успех зависит от погоды. В хорошую погоду он продает в день 1000 очков и 100 зонтиков, в пасмур­ную — 500 зонтиков. Зонтики он покупает по 50 цен­тов, продает по одному доллару; очки покупает по 20 цен­тов, продает по 50 центов. Коммерсант каждый день за­купает товар на 250 долл., а на другой день старается продать его полностью (оставшийся товар пропадает). Он не доверяет метеосводкам и считает, что господь бог назначает хорошую или плохую погоду с помощью мо­неты (орел-решка). Проблема состоит в том, чтобы сде­лать закупку оптимальным образом.

Описанную ситуацию можно рассматривать как игру с двумя игроками, причем вторым игроком является природа (или погода). Это игра 2´2, т. к. у каждого из игроков есть два хода.

У игрока А (коммерсанта):

Первый ход (А1) — закупка в расчете на дождь, второй ход (А2) — закупка в расчете на ясную погоду.

У игрока Б (природа):

Первый ход (Б1) — дождь, второй ход (Б2) — ясная погода.

В качестве платежей естественно взять выигрыш игрока А, т. е. прибыль коммерсанта. В расчете на дождь он на все 250 долл. закупает только зонтики (500 штук). Если будет дождь, то он продаст все зонтики и получит прибыль 250 долл. Если же будет ясная погода, то ему удасться продать только 100 зонтиков на 100 долл., т. е. он понесет убыток в 150 долл. Можно счи­тать, что в этом случае его прибыль отрицательная, т. е. –150 долл.

В расчете на ясную погоду коммерсант закупает на 250 долл. 1000 пар очков и 100 зонтов. В ясную погоду он все это продаст за 600 долл., т. е. получит 350 долл. прибыли. Но в дождь он сумеет продать из всего этого товара только 100 зонтов на 100 долл., т. е. понесет убы­ток в 150 долл. (или получит –150 долл. прибыли).

Матрица игры выглядит следующим образом:

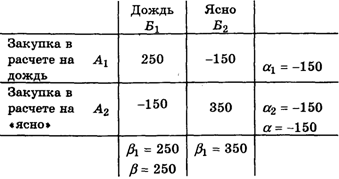
Мы видим, что a¹b, т. е. седловой точки нет. Следовательно, игрок А не может выбрать определенную стратегию и должен ходы чередовать. Далее заметим, что т. к. все числа a1, A2, B1, b2 различны, то ходы не­равноправны. Поэтому возникает вопрос: в какой про­порции их сочетать, чтобы получить оптимальную стратегию?

Теория игр дает следующее правило для определения искомой пропорции. Разность платежей, записанных в первой строке равна 400; разность платежей, записан­ных во второй строке, равна 500; отношение этих чисел равно 4:5, поэтому первый и второй ходы следует при­менять в пропорции 5:4, т. е. из каждых девяти ходов должно быть 5 первых и 4 вторых. Используя понятие частоты, введенное в гл. II, §1, мы можем сказать, что относительная частота первого хода 5/9, а второго — 4/9. Это означает, что коммерсант должен вложить 5/9 своего капитала (138,88 долл.) в товары для дождливого дня (только зонтики) и 4/9 капитала (111,12 долл.) в товары для ясного дня. Среди последних, согласно усло­вию задачи, пятую часть — 22,22 долл. — занимают зонтики. Итак, зонтиков следует закупить на 161,1 долл., очков — на 88,9 долл.

Что же получит коммерсант в результате примене­ния этой оптимальной стратегии? Теория игр дает ответ и на этот вопрос. Найдем так называемую цену игры:

250 + (–150) = 72,22$,

Которая представляет собой среднее арифметическое платежей, стоящих в первом столбце [см. формулу (4) из §1 гл. II]. Следовательно, применяя найденную опти­мальную стратегию, коммерсант будет получать устой­чивую среднюю прибыль в 72,22 долл.

Замечания.

1. В теории игр рассматриваются игры с любым числом ходов, с несколькими игроками, с несколькими платежными матрицами, с коалициями игроков, с различными правилами игры, многошаговые, динамические, иерархические игры и т. д.

2. Существуют формулы, по которым, зная возмож­ные стратегии игроков и матрицы платежей, можно найти цену игры и оптимальные стратегии для каждого игрока. В играх с большим объемом вычислений ис­пользуют ЭВМ.

3. Считается, что каждый игрок не знает о планах другого. В случае, если игроки заранее договариваются между собой о выигрыше (как некоторые футбольные клубы), то применять математические методы для вы­бора оптимальной стратегии в такой игре бессмысленно.

Задачи для самостоятельного решения

1. Полк должен атаковать и захватить одно из двух оборонительных сооружений противника. Противник может успешно оборонять лишь одно из этих сооруже­ний, но не оба сразу. Известно, что одно из сооружений в 3 раза важнее второго. Каковы оптимальные стратегии противников?

2. Скупой пассажир размышляет, купить ему билет или нет? Если он покупает билет, но контролера нет, то он теряет 1 руб. В случае, если он покупает билет и контролер его проверяет, то получается игра «вничью». За безбилетный проезд пассажир платит 10 руб. плюс стоимость проезда. В случае удачного проезда без билета пассажир считает, что получил 1 руб. прибыли. Найди­те оптимальные стратегии для пассажира и контролера и цену игры.

< Предыдущая		Следующая >