5.1. Функции и графики. Декартовы координаты
Метод координат представляет собой один из наиболее универсальных математических методов и используется для решения самых разнообразных задач. В основе метода лежит понятие Системы координат на прямой, плоскости и в пространстве.
Система координат на прямой возникла в результате осознания математиками того факта, что точек на прямой, образно говоря, столько же, сколько действительных чисел. Точнее, каждую точку на прямой можно соотнести с некоторым действительным числом (единственным!), которое называется Координатой этой точки.*
* На самом деле все обстоит сложнее. Бесконечные множества сравнивают не по количеству элементов, в них содержащихся, а с помощью Взаимно однозначного соответствия. Поэтому точнее было бы сказать, что между множеством точек прямой и множеством действительных чисел имеется взаимно однозначное соответствие.
Проще всего это сделать с помощью так называемой равномерной шкалы (вспомните термометр!):
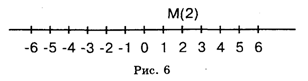
Прямую с отмеченным на ней положительным направлением называют Осью. Точка О называется Началом координат. Около каждой точки записывается ее координата.
Разделим, например, отрезок [0,1] на десять равных частей:*
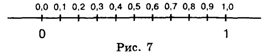
* Мы изобразили отрезок [0,1] большим, чем на предыдущем рисунке. Но мы не считаем, что он увеличился, просто мы смотрим на него сквозь увеличительное стекло.
Каждой точке деления определим координату как показано на рисунке. Точно так же делим на десять частей любой другой отрезок, концы которого отмечены целыми числами. В результате на шкале появятся точки, отмеченные координатой с одним десятичным знаком после запятой.
Далее каждый новый отрезок делим опять на десять частей, например:
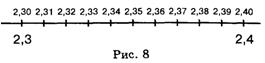
В результате появятся точки, отмеченные координатами с двумя десятичными знаками после запятой. Продолжая эту процедуру, мы получим точки, координатами которых будут дроби с тремя, четырьмя... десятичными знаками после запятой. При этом, какую бы десятичную дробь мы ни взяли, после некоторого числа шагов мы получим точку, координатой которой является эта десятичная дробь.*
* Иногда говорят так: «продолжая эту процедуру до бесконечности, мы получим все точки, координатами которых являются всевозможные десятичные дроби». Возможность продолжать процедуру деления до бесконечности — это Математическая абстракция. Здесь необходимо принять во внимание два допущения. На первое из них указал еще Евклид, определив точку так: точка это то, что не имеет частей. Во-вторых, предполагается, что при уменьшении длины отрезка все его свойства сохраняются, т. е. с меньшим отрезком можно делать все то же, что и с большим отрезком. Однако это не будет верно, если прямые и точки считать Физическими объектами. Современная физика утверждает, что бесконечно дробить нельзя, т. к. существует наименьшая величина — квант, и что свойства больших тел (макромир) отличаются от свойств малых тел (микромир).
Помимо этих точек, на прямой есть также точки, координаты которых являются бесконечными десятичными дробями.*
* Существование таких точек гарантирует аксиома Дедекинда, входящая в систему аксиом евклидовой геометрии (см. гл. VII, §2).
Как описать положение этих точек на прямой? Рассмотрим, например, точку А с координатой ![]() = 2,333.... 3
= 2,333.... 3
Бесконечная периодическая дробь ![]() удовлетворяет бесконечной последовательности неравенств:
удовлетворяет бесконечной последовательности неравенств:
2,3 < ![]() < 2,3, 2,33 <
< 2,3, 2,33 < ![]() < 2,34, 2,333 <
< 2,34, 2,333 < ![]() < 2,334,...
< 2,334,...
Поэтому точка А (7/3) находится между точками M1(2,3) и N1(2,4); между M2(2,33) и N2(2,34); между М3(2,333) и N3(2,334) и т. д. Расстояние между правой и левой точками все время уменьшается и стремится к нулю, поэтому существует Единственная точка, удовлетворяющая всем написанным выше неравенствам. Это и есть точка А (7/3).
Расстояние |MN| между точками М(х) и N(Y) прямой вычисляется через их координаты Х и У по формуле:
|MN| = |Y – х|. (1)
Самая простая и наиболее распространенная система координат на плоскости называется Декартовой по имени известного математика и философа Рене Декарта. Декартова система координат образована двумя перпендикулярными осями, осью Х и осью Y (рис. 9).

Точка пересечения осей называется Началом и служит одновременно началом координат на каждой из осей. Масштаб на осях выбирается одинаковый.* Система координат нужна для того, чтобы каждой точке плоскости соответствовали две координаты — два действительных числа Х и У. Делается это так. Спроектируем точку М на координатные оси, т. е. опустим из нее перпендикуляры на них. Обозначим основания перпендикуляров M1 и М2. Тогда Х есть координата точки М1 на оси X, а У есть координата точки M2 на оси Y. Очевидно, что
Если точка М лежит в I квадранте, то Х ³ 0, У ³ 0;
Если точка М лежит во II квадранте, то Х £ 0, У ³ 0;
Если точка М лежит в III квадранте, то Х £ 0, У £ 0;
Если точка М лежит в IV квадранте, то Х ³ 0, у £ 0;
Если точка М лежит на оси X, то У = 0;
Если точка М лежит на оси Y, то Х = 0;
Начало О имеет координаты (0,0).
* Иначе система координат будет называться Аффинной, а не декартовой.
УПРАЖНЕНИЯ
1. Если точка М лежит в верхней полуплоскости, т. е. выше оси X, то ее координаты удовлетворяют неравенству... ;
Если точка М лежит в нижней полуплоскости, т. е. ниже оси X, то ее координаты удовлетворяют неравенству... ;
Если точка М лежит в правой полуплоскости, т. е. справа от оси Y, то ее координаты удовлетворяют неравенству... ;
Если точка М лежит в левой полуплоскости, т. е. слева от оси Y, то ее координаты удовлетворяют неравенству....
2. Постройте точки с координатами (1,1), (-1,1), (1,-1),(-1,-1).
3. Опишите часть плоскости, в которой находятся точки с координатами
![]()
В школе Вы доказывали, что расстояние между двумя точками плоскости М1(Х1,у1) и М2(Х2,у2) вычисляется по формуле
![]() . (2)
. (2)
Доказательство основано на применении теоремы Пифагора к треугольнику M1M2M (см. рис. 10).

УПРАЖНЕНИЯ
4. Найдите расстояние между точками М1(1,2) и М2(3,4); M1(l,–2) и М2(–3,4); M1(l,3) и М2(1,–7); М1(3,5) и М2(–1,5).
Отметьте эти точки на чертеже.
5. Укажите все точки с целыми координатами, находящиеся внутри круга радиуса 2 с центром в начале координат, и отметьте их на чертеже. Найдите расстояния от этих точек до начала координат и округлите результаты до 0,01.
| < Предыдущая | Следующая > |
|---|