2.1. Первичная обработка результатов эксперимента. Среднее арифметическое

Явления, происходящие в природе, обществе, челове­ке очень сложны и разнообразны. Ученые изучают раз­ные стороны этих явлений, причем каждая наука выра­батывает свои специфические методы исследования. На­пример, такое важное социальное явление как преступ­ность изучают не только юристы, но и социологи, психо­логи, медики и т. д. Есть тут серьезная работа и для ма­тематиков. Их задача состоит, например, в том, чтобы подвергнуть математической обработке огромный статис­тический материал — отчеты органов внутренних дел и любые другие документы, содержащие различные число­вые данные. Цель этой работы — выделить наиболее су­щественные сведения об интересующем нас явлении.

Результаты обработки представляют в виде таблиц, графиков, диаграмм и различных числовых характерис­тик, которые называют параметрами. Важнейшие из них — Среднее арифметическое и Дисперсия.

Понятие Среднего значения используется для описа­ния разнообразных явлений природы и общественной жизни. Так, говорят о средней температуре воздуха, средней скорости движения, средней зарплате, средней продолжительности жизни и т. д. В науке и технике на основе взаимоотношений между средними величинами изучают и рассчитывают всевозможные проекты, в эко­номике — оптимальные планы, в военном деле — воз­можные стратегии и основанные на них военные док­трины, в общественной жизни — прогнозы обществен­но-политической ситуации. Например, во время пред­выборной кампании службы по изучению общественного мнения составляют прогнозы, в которых оценивают шансы на успех различных кандидатов. Ясно, что про­вести опрос всех избирателей невозможно, поэтому про­водят опрос небольшой части населения. По результатам опроса прогнозируют средние проценты популярности кандидатов у различных социальных групп и в разных регионах. Если обработка результатов опроса проведена математически грамотно, то выводы будут достаточно точно отражать реальную ситуацию.

Средней величиной обычно называют Среднее ариф­метическое.

Пусть Х1, х2, ... , хN — некоторые числа. Их Средним арифметическим называется число

(1)

Пример 1. По сведениям автоинспекции, количество дорожных происшествий на улицах города Дрюкова в первую декаду октября было таким:

6 8 10 7 6 11 9 8 7 11.

Среднее арифметическое этих чисел

Показывает среднее число дорожных происшествий в день.

В сводке за следующие 10 дней оказались такие данные:

0 5 7 7 12 11 14 13 7 6.

Их среднее арифметическое будет

Мы видим, что средние значения (8,2 и 8,3) отличаются друг от друга значительно меньше, чем число происше­ствий за каждый день, которое может быть 0, 5, 7, ...14. Поэтому Среднее число дорожных происшествий можно прогнозировать, причем достаточно точно.*

* Конечно, средние величины могут различаться, и довольно значительно. Например, количество дорожных происшествий зависит от погоды, времени года, солнечной активности и от многих других факторов. Однако свойство средних величин состоит в том, что различие между ними все-таки меньше, чем различие между исходными данными.

Этот факт подтверждается и отчетами ГАИ за много лет. Из них видно также, что чем больше срок, за кото­рый составляется отчетность (декада, месяц, квартал, год, пятилетка), тем средняя величина устойчивее. Иными словами, среднее число происшествий за декаду колеблется меньше, чем число происшествий за каждый день; среднее число происшествий за месяц колеблется еще меньше, и так далее.

Описанное свойство средних представляет собой одно из важнейших проявлений Закона Больших Чисел, откры­того знаменитым русским математиком П. Л. Чебышевым.

Если таблица исходных данных содержит несколько десятков чисел, то составляют более сложную таблицу, в которой для каждой из величин указывают, сколько раз она наблюдалась.

Пример 2. УВД города Дрюкова опубликовало свод­ку о числе правонарушений, совершенных подростками за первые 20 дней сентября: 8 6 13 4 13 13 12 9 7 6 12 14 13 12 17 6 8 12 7 12.

По этим данным составлена следующая таблица:

Таблица 1

Здесь Mi — число дней с одним и тем же количе­ством правонарушений, — число правонарушений за день. Из таблицы видно, например, что был всего 1 день, в течение которого произошло ровно 4 правонарушения; в течение трех дней было по 6 правонарушений и т. д. Заметьте, что в первой строке числа расположены в порядке возрастания, а если сложить все числа второй строки, то получится общее число дней, т. е. 20.

Согласно приведенным данным, среднее число пра­вонарушений за один день будет

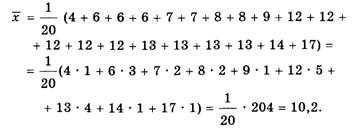
Таким образом, формулу (1) для подсчета среднего арифметического можно записать так:

Здесь — различные среди заданных N чи­сел, причем значение встречается Т1 раз, значение повторяется Т2 раз, и так далее, наконец, значение встречается ТK раз. При этом

M1 + M2 + ... + mk = N.

Табл. 1 можно переписать так, чтобы в ней не содержалась информация о числе дней, в течение которых про­водились наблюдения. Заменим в табл. 1 вторую строку на новую, которую составим так: вместо числа дней по­ставим долю, которую это число составляет от числа всех дней. Эта доля называется Частотой. Так как число всех дней 20, то 1 заменим на 1/20 = 0,05, 3 — на 3/20 = 0,15 и т. д. В результате табл. 1 примет следующий вид:

Таблица 2

Как и в табл. 1, в первой строке указано число пра­вонарушений за день, а во второй — соответствующая частота. Сумма чисел, стоящих во второй строке, равна единице. Это свойство следует из определения частоты.

Используя понятие частоты, мы можем подсчитать среднее значение Х [см. (2)] иным способом:

Таким образом, Среднее арифметическое равно сумме произведений чисел, взятых из первой строки табл. 2, на их частоты.

Преобразуем таким же способом формулу (3). Введем частоты

В результате формула (3) для среднего арифметического запишется так:

Преимущество этой формулы, по сравнению с формулой (3), состоит в том, что ей можно пользоваться и в том случае, когда не известны величины Т1, т2, ..., тK и N, но известны значения частот.

Пример 3. В городе Дрюкове каждому пассажиру междугородного автобуса вручают страховой полис на 50 000 руб., взимая за это 500 руб. Какова средняя при­быль страховой компании от продажи одного полиса, если несчастные случаи происходят в среднем с одним пассажиром из 10 000? Учтите, что по правилам страхо­вых компаний города Дрюкова страховка выплачивает­ся только в случае гибели пассажира.

Решение. Прибыль может принимать два значения:

500 руб, если несчастного случая не произошло, и –49 500 руб. при автокатастрофе (знак «минус» означа­ет, что компания терпит убыток). Прибыль -49 500 руб. рублей появляется в одном случае из 10 000, следова­тельно, частота этого значения прибыли равна 0,0001. Частота другого значения — 500 руб. равна 0,9999. По­лучаем следующую таблицу:

Среднее значение прибыли найдем по формуле (4):

< Предыдущая		Следующая >