075. Способы построения графиков функций

Анализ графиков элементарных функций показывает, что если известен график функции , то при помощи геометрических преобразований можно построить график более сложной функции.

Рассмотрим некоторые способы построения графиков при помощи геометрических преобразований.

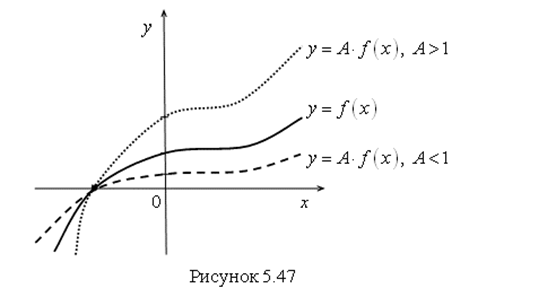
1. График функции получается из графика увеличением всех ординат этого графика в раз, если и уменьшение ординат графика в раз, если (рис. 5.47).

Пример 3. Постройте график функции .

Решение. Сначала построим график функции .

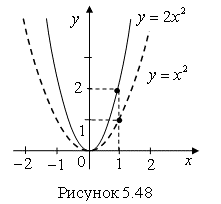
Увеличим все ординаты этого графика в 2 раза и получим график функции (рис. 5.48).

Ответ. График функции показан на рис. 5.48 сплошной линией.

2. График функции получается из графика сжатием графика вдоль оси , если и растяжением графика вдоль оси , если .

Пример 4. Постройте графики функций и .

Решение. Составим таблицу некоторых значений функций и (табл. 5.3).

Таблица 5.3 – Значения функций , ,

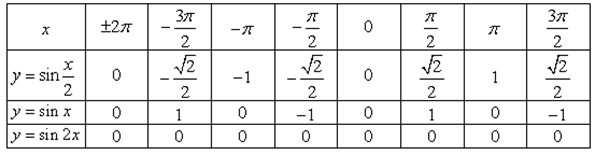
Для функции основным периодом будет . Тогда основной период функции равен , а основной период функции равен .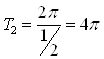

По данным таблицы 5.3 построим графики всех трех функций (рис. 5.49).

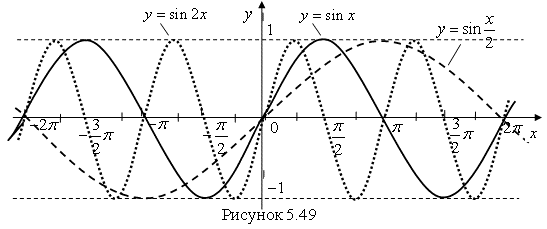
Вывод. Из графика функции сжатием его вдоль оси получается график функции , а график функции получается растяжением графика функции вдоль оси

Ответ. График функции показан на рис. 5.49 точечной линией. График функции показан на рис. 5.49 пунктирной линией.

3. График функции Получается сдвигом графика вдоль оси на величину влево (в отрицательном направлении оси ), если и вправо (в положительном направлении оси ), если .

Пример 5. Постройте графики функций и .

Решение. Составим таблицу некоторых значений функций и (табл. 5.4).

Таблица 5.4 – Значения функций , ,

	–4	–3	–2	–1	0	1	2	3	4
	36	25	16	9	4	1	0	1	4
	16	9	4	1	0	1	4	9	16
	4	1	0	1	4	9	16	25	36

Построим графики этих функций по данным таблицы 5.4 (рис. 5.50).

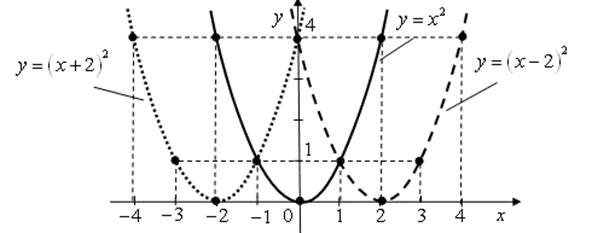
Вывод. График функции получается сдвигом графика на 2 единицы вдоль оси влево (в отрицательном направлении оси ), а график функции получается сдвигом графика на 2 единицы вдоль оси вправо (в положительном направлении оси ).

Ответ. График функции показан на рис. 5.50 точечной линией. График функции показан на рис. 5.50 пунктирной линией.

Пример 6. Постройте график функции .

Решение. Сначала построим график функции . Сдвинем его на 3 единицы влево (по правилу построения графика функции ). При этом вертикальная асимптота гиперболы тоже сдвинется на 3 единицы влево. Следовательно, график функции имеет две асимптоты: и . Найдем координаты точки пересечения графика с осью : ; .

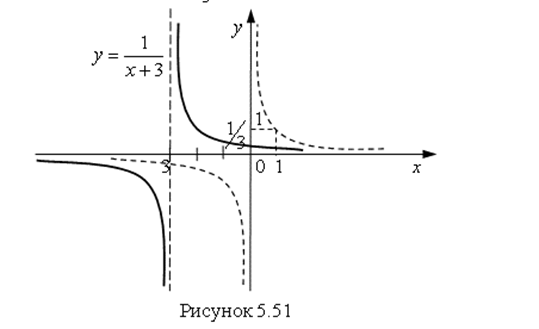
Ответ. График функции показан на рис. 5.51 сплошной линией.

4. График функции Получается сдвигом графика на величину в положительном направлении оси (вверх), если и в отрицательном направлении оси (вниз), если .

Пример 7. Постройте графики функций и .

Решение. Составим таблицу некоторых значений функций , и (табл. 5.5).

Таблица 5.5 – Значения функций , ,

	–3	–2	–1	0	1	2	3
	7	2	-1	-2	-1	2	7
	9	4	1	0	1	4	9
	11	6	3	2	3	6	11

Построим графики этих функций по данным таблицы 5.5 (рис. 5.52).

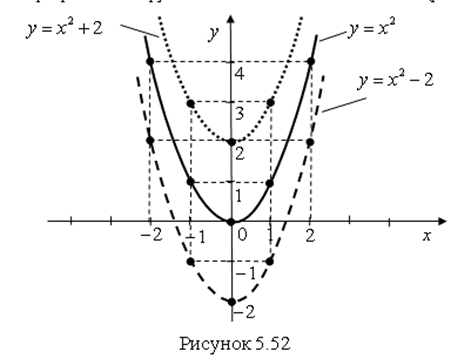
Вывод. График функции получается сдвигом графика на 2 единицы вниз вдоль оси а график функции получается сдвигом графика на 2 единицы вверх вдоль оси .

Ответ. График функции показан на рис. 5.52 пунктирной линией. График функции показан на рис. 5.52 точечной линией.

Пример 8. Постройте график функции .

Решение. Сначала построим график функции . Сдвинем его на 2 единицы вниз (по правилу построения графика функции ). При этом горизонтальная асимптота гиперболы тоже сдвинется на 2 единицы вниз. Следовательно, график функции имеет две асимптоты: и . График функции пересекает ось .
При получим: , т. е. (рис. 5.53).

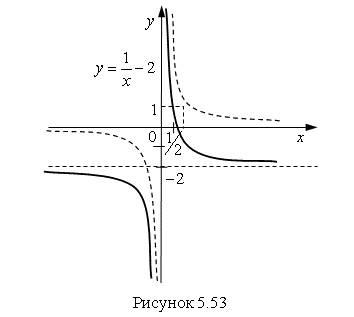
Ответ. График функции показан на рис. 5.53 сплошной линией.

5. График функции Получается симметричным отображением графика функции относительно оси .

Пример 9. Постройте графики функций и .

Решение. Составим таблицу некоторых значений этих функций (табл. 5.6).

Таблица 5.6 – Значения функций та

	1	2	3	4	5
	6	3	2	3	6
	-6	-3	-2	-3	-6

Построим графики этих функций по данным таблицы 5.6 (рис. 5.54).

Вывод. График функции получается симметричным отображение графика относительно оси .

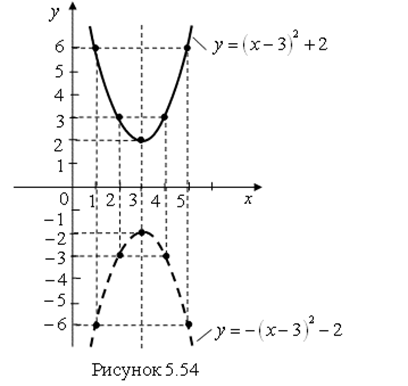
Ответ. График функции показан на рис. 5.54 сплошной линией. График функции показан на рис. 5.54 пунктирной линией.

Пример 10. Постройте график функции .

Решение. Построим одну полуволну графика функции . Произведем ее сжатие вдоль оси с коэффициентом 3 и растяжение вдоль оси с коэффициентом 2, а затем симметричное преобразование относительно оси Получим график функции (рис. 5.55 а).

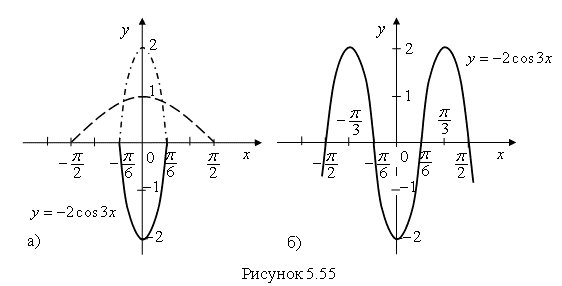
На рисунке 5.55 а показана одна полуволна графика, а на рисунке 5.55 б – весь график.

Ответ. График функции показан на рис. 5.55 (б) сплошной линией.

6. График функции получается симметричным отображением графика функции относительно оси .

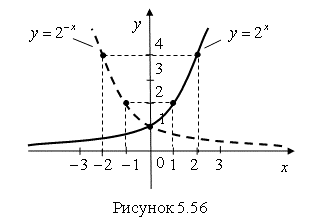
Пример 11. Постройте графики функций и .

Решение. Составим таблицу некоторых значений этих функций (табл. 5.7).

Таблица 5.7 – Значения функций та

	–3	–2	–1	0	1	2	3
				1	2	4	9
	9	4	2	1

Построим графики этих функций по данным табл. 5.7 (рис. 5.56).

Вывод. График функции получается симметричным отображение графика относительно оси .

Ответ. График функции показан на рис. 5.56 сплошной линией. График функции показан на рис. 5.56 пунктирной линией.

Пример 12. Постройте график функции .

Решение. Строим график функции и симметрично отображаем его относительно оси .

Ответ. График функции показан на рис. 5.57 сплошной линией.

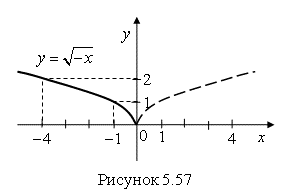
7. График функции получается из графика функции симметричным отображением относительно оси части графика, которая лежит под осью (). Часть графика над осью () остается без изменений.

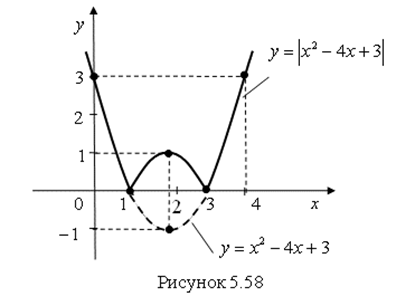
Пример 13. Постройте график функции .

Решение. Составим таблицу некоторых значений функции (табл. 5.8).

Таблица 5.8 – Значения функции

	0	1	2	3	4
	3	0	-1	0	3

Из решения уравнения находим, что нулями функции будут два значения: и .

Найдем координаты вершины параболы:

; .

По полученным результатам построим график функции (рис. 5.58).

Интервалами положительности для этой функции будут интервалы . Интервалом отрицательности будет .

Из определения модуля функции запишем:

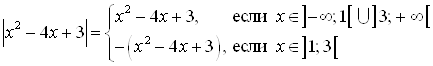
На интервале значения функций и совпадают и по величине и по знаку, а на интервале значения функций совпадают по величине, но противоположны по знаку.

Вывод. График функции получается из графика функции симметричным отображением относительно оси той части графика, которая лежит ниже оси .

Ответ. График функции показан на рис. 5.58 сплошной линией.

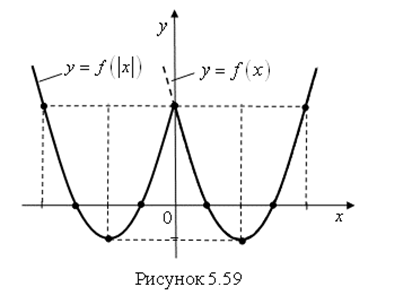
8. График функции получается из графика функции так: график функции сохраняется только при , и отображается симметрично относительно оси (рис. 5.59).

Пример 14. Постройте график функции .

Решение. Учитывая определение модуля, функцию можно записать так:

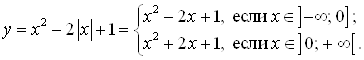
Составим таблицу значений функции по этим формулам на соответствующих интервалах (табл. 5.9).

Таблица 5.9 – Значения функции

	-3	-2	-1	0	1	2	3
	4	1	0	1	0	1	4

По данным этой таблицы построим график функции (рис. 5.60).

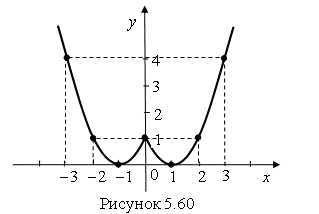
Вывод. Как видно из рис. 5.60 график функции получается из графика функции симметричным отображение части графика при относительно оси .

Ответ. График функции показан на рис. 5.60 сплошной линией.

Пример 15. Постройте график функции .

Решение. Заданная функция содержит как модуль аргумента, так и модуль функции.

Перепишем формулу заданной функции в виде: .

Построим параболу квадратичной функции без модуля аргумента. Это будет график функции , смещенный на 1 вправо вдоль оси и на 4 вниз вдоль оси . Осью симметрии графика будет прямая . Координатами вершины параболы будут и (рис. 5.61).

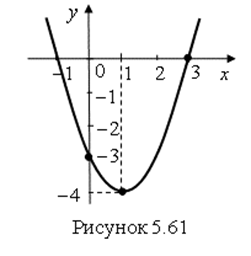
График функции будет получен из графика симметричным отображением части графика при относительно оси (рис. 5.62).

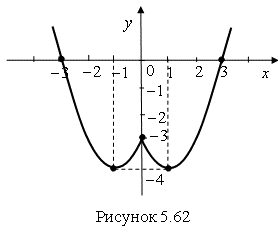
График модуля функции получается симметричным отображением относительно оси части графика функции , которая находится под осью (рис. 5.63).

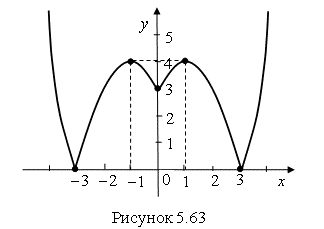
Ответ. График функции показан на рис. 5.63 сплошной линией.

< Предыдущая		Следующая >