008. Простые и составные числа. Разложение чисел на простые множители. НОД и НОК. Признаки делимости чисел
Частное двух чисел может быть: точное и неточное.
, 
, 
, Где 
– это делимое; 
– это делитель; 
– это частное; 
– это остаток.
Делитель числа – это число , на которое число делится без остатка (
).
Кратное числа – это число, которое делится на число без остатка ().
Например, 
. Число 3 – это делитель числа 21; а число 21 – это кратное числа 3.
Числа 1, 2, 3, 4, 5 … – это Натуральные числа. Число 0 – это не натуральное число.
Числа 2, 3, 5, 7, 11, 19, 23 … делятся только на единицу (1) и сами на себя. Это простые числа.
Простые числа – это числа, которые имеют только два делителя.
Например, число 23 – это простое число, потому что 23 делится только на "1" и на "23". Следовательно, число 23 имеет только два делителя 1 и 23, то есть: 
; 
.
Числа 4, 6, 8, 9, 10, 12 … делятся на "1", сами на себя и на другие числа. Это составные числа.
Составные числа – это числа, которые имеют больше двух делителей.
Например, число 36 делится на 1, 2, 3, 4, 6, 9, 12, 18, 36. Следовательно, число 36 имеет девять делителей.
1 (единица) – не простое и не составное число.
Составные числа можно разложить на простые множители.
Разложить число на простые множители – это значит записать его как произведение простых чисел.
Пример 4. Разложите число 27 на простые множители.
Ответ. Числа 2, 2, 3 – это простые множители.
Общий делитель нескольких чисел – это число, на которое все данные числа делятся без остатка.
Например, число 18 делится на 2, 3, 3; число 24 делится на 2, 2, 2, 3. Общие делители чисел 18 и 24 – это 2 и 3. Среди всех делителей всегда есть наибольший. Так, наибольший делитель чисел 18 и 24 – это 6 (
).
Наибольший общий делитель Нескольких чисел (НОД) – это самое большое натуральное число, на которое делится каждое из данных чисел без остатка.
Пример 5. Найдите НОД чисел 45, 60, 75.
Решение. Разложим числа 45, 60, 75 на простые множители.
Числа 3 и 5 – это общие множители.
Ответ. 
.
Наименьшее общее кратное (НОК) нескольких чисел – это самое меньшее натуральное число, которое делится на каждое из данных чисел без остатка.
Пример 6. Найдите НОК чисел 5, 6 и 8.
Решение. Разложим числа 5, 6 и 8 на простые множители.
. 
.
Ответ. 
.
Пример 7. Найдите НОК чисел 72 и 108.
Решение. Разложим числа 72 и 108 на простые множители.
; 
.
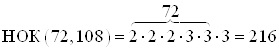
Ответ. 
.
Пример 8. Найдите НОК чисел 360 и 70.
Решение. 
. Используем формулу:
.
Ответ. 
.
Пример 9. Найдите НОК чисел 20 и 27.
Решение. Разложим числа 20 и 27 на простые множители:
; 
.
Числа 20 и 27 не имеют общих множителей, значит:
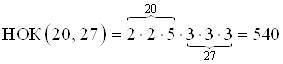
Ответ. 
.
НОК чисел, которые не имеют общих множителей – это произведение этих чисел.
Таблица 1.10 – Признаки делимости чисел
|
Делимость чисел |
Признаки делимости чисел |
Примеры |
|
На "2" |
Последняя цифра числа делится на 2 или равна нулю |
12, 50, 348, 576, 4294, 30590 … |
|
На "5" |
Последняя цифра числа равна 5 или нулю |
15, 80, 375, 1005 … |
|
На "3" |
Сумма цифр числа делится на 3 |
156, 222, 378, 1032, 15189 … |
|
На "9" |
Сумма цифр числа делится на 9 |
153, 252, 819, 3150, 5787 … |
|
На "4" |
Число, которое состоит из двух последних цифр данного числа, делится на 4 или две последние цифры числа – нули |
112, 600, 724, 1084, 3048 … |
|
На "25" |
Число, которое состоит из двух последних цифр данного числа, делится на 25 или две последние цифры числа – нули |
250, 400, 975, 1050, 5125 … |
|
На "8" |
Число, которое состоит из трех последних цифр данного числа, делятся на 8 или три последние цифры числа – нули |
1008, 3032, 5120, 9000 … |
|
На "125" |
Число, которое состоит из трех последних цифр данного числа, делится на 125 или три последние цифры числа – нули |
1375, 10125, 51000 … |
|
На "6" |
Число делится на 2 и на 3 |
126, 348, 750, 1068, 3163, 17844 … |
|
На "7", "11", "13" |
Разность между числом, которое состоит из трех последних цифр данного числа, и числом, которое состоит из остальных цифр этого числа, делится на 7, 11 или 13 |
1071; 55258 делятся на 7; 28501; 1353 делятся на 11; 1157; 5928 делятся на 13 |
| < Предыдущая | Следующая > |
|---|
