03. Среднее арифметическое

Понятие среднего значения используется для описания разнообразных явлений природы и общественной жизни: средняя температура воздуха, средняя зарплата, средняя продолжительность жизни. Например, для изучения общественного мнения проводят опрос не всех избирателей, а лишь небольшой части населения. По результатам прогнозируют популярность кандидатов у различных групп населения в разных регионах. При грамотной математической обработке результатов опроса выводы будут достаточно точно отражать реальную ситуацию.

Средней величиной обычно называют среднее арифметическое.

Пусть - некоторые числа. Их средним арифметическим называется число

(1)

Пример. Количество ДТП на улицах города в первую декаду декабря:

6 8 10 7 6 11 9 8 7 11. Среднее арифметическое этих чисел

Показывает среднее число ДТП в день.

В сводке за следующие 10 дней такие данные: 0 5 7 7 12 11 14 13 7 6.

Их среднее арифметическое

Отсюда видно, что средние значения 8,3 и 8,2 отличаются друг от друга значительно меньше, чем число ДТП за каждый день. Поэтому среднее число ДТП можно прогнозировать, причем достаточно точно. Этот факт подтверждается и отчетами ГАИ за много лет. Из них также видно, что чем больше срок отчетности (декада, месяц, квартал, …), тем устойчивее средняя величина.

Такое свойство средних значений представляет собой одно из важнейших проявлений закона больших чисел, открытого знаменитым русским математиком П. Л.Чебышевым.

Если исходные данные содержат несколько десятков чисел, то составляют таблицу, в которой указывают для каждой величины, сколько раз она наблюдалась.

Пример. Число правонарушений в городе, совершенных подростками за первые 20 дней сентября: 8 6 13 4 13 13 12 9 7 6 12 14 13 12 17 6 8 12 7 12. По этим данным составим таблицу:

Таблица 1

	4	6	7	8	9	12	13	14	17
	1	3	2	2	1	5	4	1	1

Здесь - число дней с одинаковым количеством правонарушений, - число правонарушений за день. В первой строке значения расположены в порядке возрастания, а если сложить все числа второй строки, то получится общее число дней, т. е. 20.

Среднее число правонарушений в день:

.

Отсюда формулу (1) можно переписать так:

(2)

Здесь - различные среди заданных n чисел. При этом

(3)

Таблицу 1 можно переписать так, чтобы во второй строке вместо числа дней стояла доля, которую это число составляет от числа всех дней, т. е. частота:

Таблица 2.

	4	6	7	8	9	12	13	14	17
	0,05	0,15	0,1	0,1	0,05	0,25	0,2	0,05	0,05

Используя понятие частоты, подсчитаем среднее значение иным способом:

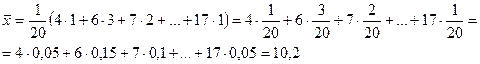
Таким образом, среднее арифметическое равно сумме произведений чисел, взятых из первой строки таблицы 2, на их частоты.

Преобразуем таким же способом формулу(2). Возьмем частоты:

;;…;

Отсюда

(4)

Этой формулой можно пользоваться и в том случае, когда не известны величины , но известны значения частот.

Пример. В некотором городе каждому пассажиру междугородного автобуса вручают страховой полис на 50000 руб., взимая за это 50 руб. Какова средняя прибыль страховой компании от продажи одного полиса, если несчастные случаи происходят в среднем с одним пассажиром из 10000?

Решение. Прибыль может принимать 2 значения: 50 руб., если несчастного случая не произошло, и – 49950 руб. при гибели пассажира. Составим таблицу частот:

Прибыль	50	-49950
Частота	0,9999	0,0001

Отсюда среднее значение прибыли:

(руб.)

< Предыдущая		Следующая >