10. Классическое определение вероятности
Вероятность представляет собой количественную характеристику возможности наступления некоторого случайного события.
Рассмотрим испытания, в результате которого может появиться событие А. Каждый исход, при котором осуществляется событие А, называется Благоприятным событию А
Например, событие А – «четное число очков при одном бросании игральной кости». Из шести равно возможных исходов (от 1 до 6) три исхода (2, 4, 6) являются благоприятными событию А.
Вероятностью события А называется отношение числа исходов, благоприятных событию А, к числу всех исходов испытания.
Обозначается вероятность события А Через Р (А), т. е.
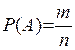 ,
,
Где M - число элементарных исходов, благоприятных А, N - число всех исходов.
Здесь предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу. Из определения вероятности вытекают следующие ее свойства:
1) Вероятность достоверного события равна единице: Р (W) = 1.
2) Вероятность невозможного события равна нулю: Р (ø) = 0
3) Вероятность случайного события заключена между нулем и единицей, т. е. 0 ≤ P (A) < 1
При решении задач на вычисление вероятностей возникают трудности, связанные с определением числа тех или иных исходов испытания. В таких случаях используют комбинаторные формулы.
Пример. Преступник знает, что шифр сейфа состоит из цифр 1, 3, 7, 9, но не знает, в каком порядке их набирать. Определить вероятность того, что первые 2 цифры шифра будут набраны верно, а также вероятность того, что сейф будет открыт с первой попытки.
Решение. В первом случае исходом будет упорядоченная пара первых двух цифр шифра. Число таких пар равно числу размещений из 4 – х элементов по 2, ![]() . Только один исход является благоприятным, и его вероятность равна 1/12. Во втором случае исходом является перестановка из цифр 1, 3, 7, 9. Число всех исходов
. Только один исход является благоприятным, и его вероятность равна 1/12. Во втором случае исходом является перестановка из цифр 1, 3, 7, 9. Число всех исходов ![]() . Только один исход является благоприятным, поэтому вероятность открыть сейф с первой попытки равна 1/24.
. Только один исход является благоприятным, поэтому вероятность открыть сейф с первой попытки равна 1/24.
| < Предыдущая | Следующая > |
|---|