12. Математическое ожидание и его свойства

Характеристика случайной величины в виде таблицы или Функции распределения представляет полное задание случайной величины Однако для разрешения ряда вопросов в теории вероятностей и К Статистике с успехом применяется более простая характеристика случайной величины - ее среднее значение X, или, что то же, математическое ожидание - М(Х)=а.

Пусть дана таблица распределения случайной величины с конечным числом возможных значений:

Введем следующее определение: Средним значением, или математическим ожиданием, случайной величины называется сумма произведений всех возможных значений случайной ВЕличины на соответствующие вероятности:

Или

Здесь важно отметить, что , А это показывает, что ИСчерпываются все возможные значения случаЙНоЙ величины, составляющие полную систему событий.

Пример 4. Проводится беспроигрышная лотерея на 200 выигрышей, из которых 1 выигрыш составляет 100 руб., 5 выигрышей по 20 руб., 10 выигрышей по 5 руб. и 184 выигрыша по 2 руб. Определить справедливую цену одного билета, рассчитанную так, чтобы сумма выплаченных выигрышей равнялась сумме, вырученной за продажу билетов.

Решение. Для применения формулы среднего значения случайной величины мы предварительно составляем в соответствии с данными о количестве отдельных выигрышей таблицу распределения:

Поэтому

Таким образом, справедливая цена одного лотерейного билета должна составить 3 руб. 09 коп.

Пример 5. Найти среднее значение числа попаданий в мишень при 6 выстрелах, если дана вероятность попадания прИ отдельном выстреле

Решение. Распределение случайной величины (числа попаданий X) в этом примере подчиняется биномиальному закону:

После вычисления соответствующих членов биномиального распределения по формуле

Имеем

Переходя к основным свойствам математического ожидания случайных величин, введем понятие об их независимости.

Определение. Случайные величины Х и Y называются независимыми, если законы распределения каждой из них не меняются, когда становится известным, что другая приняла какое-либо одно (безразлично какое) значение.

Примером двух независимых случайных величин могут служить суммы выигрышей по каждому из двух билетов по двум различным денежно-вещевым лотереям.

Здесь ставший известным размер выигрыша по билету одной лотереи не влияет на ожидаемый размер выигрыша и соответствующую ему вероятность по билету другой лотереи.

В виде другого примера независимых случайных величин можно привести данные о числе километров суточного пробега для двух машин из различных гаражей.

Свойство 1°. Математическое ожидание постоянной величины равно этой же постоянной величине.

В самом деле, таблица распределЕНия для постоянной величины С имеет вид:

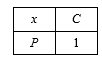
Поэтому

Свойство 2°. Математическое ожидание суммы случаЙНых величИн равно сумме их математических ожиданий.

Пусть две случайные величины Х и Y заданы соотвЕТствуЮщИми таблицами распределения.

Докажем, что .

Рассмотрим простейший случай, когда каждая из случайных величин принимает лишь по два значения:

В этих условиях сумма Х+у как случайная величина Характеризуется следующей таблицей:

Здесь произведения вида обозначают вероятности соответствующих значений суммы случайных величин Х+Y, так как эти вероятности определяются по теореме умножения вероятностей.

В самом деле, обозначает вероятность того, что и , т. е. имеет место совместное наступление двух событий: 1) случайная величина Х принимает значение и 2) случайная величина Y принимает значение .

ПоэтОМу , где и

Отсюда

Переходя к математическому ожиданию рассматриваемой сУммы, Имеем

Раскрывая в правой части скобки и группируя слагаемые по каждому значению случайной величины, получаем

Заметив далее, что суммы в каждой скобке определяют соответственные вероятности значений и , имеем

Это свойство можно распространить на любое конечное Число Слагаемых, т. Е.

Или

Это свойство справедливо и для независимых, и для зависимых случайных величин, хотя приведенное доказательство применимо лишь для независимых случайных величин.

Пример 6. Проверить свойство 2° для двух независимых случайных величин Х и Y, заданных следующими распределениями:

Решение. Составляем распределение суммы :

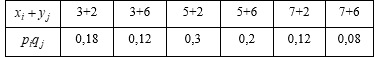
Отсюда

Определим теперь математическое ожИДанИЕ каждой из заданных случайных величин:

Таким образом, 4.8+3.6 = 8.4, чем подтверждается свойстВО Математического ожидания суммы случайных величин.

Пример 7. Найти математическое ожидание чисЛА Т Появлений События А в П повторных испытаниях, если вероятность Появления Его в отдельном испытании равна Р.

РЕШеНИЕ. Здесь число появлений события А в каждом Испытании представляет собой случайНую величину со следующим распределением:

Математическое ожидание этой случайнОй величины в каждом Испытании одинаково:

Число Т появлений события А в П испытаниях Представляет Собой также случайную величину, являющуюся суммой случайных величин :

Применяя поэтому к числу Т свойство 2° математического Ожидания суммы случайных величин, получаем

.

Так как каждое из этих П слагаемых равно Р, то Или

Заметим, что результат этого примера позволяет сразу находитЬ Среднее значение числа Т для любого случая биномиального распределения, не прибегая к сложному вычислению, проведенному в примере 5.

В отношении математического ожидания суммы случайных величин применение свойства не связано с вопросом о зависимости или независимости случайных величин. Следующая теорема—о математическом ожидании произведения случайных величин—применима только к независимым случайным величинам.

Свойство 3°. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

Пусть Х и Y—Две независимые случайные величины, таблИЦы распределения которых даются ниже:

Докажем, что .

Рассматривая XY как случайную величину, мы устанаВЛиваем, что она принимает все значеНИя вИДа , число которых опредеЛЯется произведением Kl. Вероятность каждого значения произведеНИя находится по теореме умножения вероятностей: .

Поэтому .

< Предыдущая		Следующая >