05. Теорема умножения вероятностей

События А и В называются НеЗАвисимыми, если появление или непоявление одного из них не изменяет вероятности появления другого.

ПримЕР 6. В одной урне находятся 10 шаров, из которых 5 белых; в другой — 12 шаров, из которых 8 белых. Обозначим событие, состоящее в появлении из первой урны белого шара, через А, А такое же событие, относящееся ко второй урне, через В. В этих условиях А и В — События независимые, а поэтому

а

Пример 7. Бросают две игральные кости. Факт появления некоторой грани на первой кости обозначим через А, факт появления одной определенной грани на второй кости обозначим через В.

События А и В здесь независимые, причем и

Пример 8. Из урны, в которой среди 10 шаров имеется 6 белых, извлекается один шар. Пусть А означает факт появления белого шара. Очевидно, . После фиксирования результата белый шар возвращается в ту же урну. Затем выполняется вторичное извлечение одного шара. Пусть В означает факт вторичного появления белого шара. Очевидно, и . События А и В здесь независимы, так как вероятность вторичного извлечения белого шара не зависит от того, какой шар — белый или небелый — был извлечен в первый раз.

Введем в последний пример следующее изменение. Пусть после первого извлечения шара из урны его не кладут обратно в урну, и вторичное извлечение шара из урны, имеющее своим результатом событие В, проходит в измененных условиях: общее число шаров в урне составляет уже не 10, а 9, и число исходов, благоприятствующих появлению белого шара, связано с цветом невозвращенного шара. Если этот шар белый, то условия для появления белого шара состоят в наличии 5 благоприятствующих исходов из 9 возможных; это дает . Если же невозвращенный шар небелый, то при вторичном извлечении шара из урны появлению белого шара БлагоприятСтвуют 6 исходов из 9 возможных, что дает .

При описанных новых условиях события А и В оказываются уже зависимыми, так как на вероятность появления события В влияет имевший место исход в отношении события А: Р(В) имеет одно значение при появлении события А и — другое при непоявлении его. Таким образом, вероятность появления события В носит условный характер и поэтому называется Условной вероятностью.

Условная вероятность появления события В, если произошло событие А, обозначается символом .

В рассматриваемом примере имеем

И

Теорема. Вероятность совместного наступления двух событий равна произведению вероятности наступления первого события на условную вероятность наступления второго события, вычисленную в предположении, что первое событие имеет место.

Доказательство. Пусть из общего числа П исходов (несовместимых, единственно возможных и Равновозможных) испытания наступлению события А благоприятствуют K исходов испытания, а наступлению события В благоприятствуют L исходов из числа K Исходов, благоприятствующих наступлению события А. Это значит, что совместному наступлению событий А и В благоприятствует L Исходов из общего числа их П.

Поэтому

Простое преобразование полученной дроби

Позволяет выразить искомую вероятность в виде

Но первый множитель представляет вероятность наступления события А, т. Е. , а второй множитель выражает вероятность наступления события В при условии, что произошло событие A, Т. е. .

Отсюда

Что и доказывает теорему.

Полученный результат для вероятности совместного наступлеНиЯ двух зависимых событий легко переносится на СЛучай, когда события А и В независимы.

В самом деле, в этом случае вероятность появления события В Не зависит от исхода испытания в отношении события А, т. Е. Здесь имеет место

.

Поэтому для независимых событий А и В

.

Пример 9. Найти вероятность двукратного извлечения белого шара из урны, в которой из 12 шаров имеется 7 белых: а) если вынутый шар возвращается обратно в урну и б) если вынутый шар в урну не возвращается.

Решение. Обозначая появление белого шара первый раз символом А и второй раз символом В, будем иметь:

А) события А и В независимы и

Поэтому

Б) события А и В зависимы и

а

Поэтому

Теорема умножения вероятностей обобщается для трех, четырех и т. Д. зависимых событий. В частности, имеют место следующие формулы:

Здесь символ означает условную вероятность появления события С, если произошли события А и В, а символ — Условную вероятность появления события D, если произошли события А, В и С.

Соответственно для независимых событий имеют место следующие формулы:

И

Пример 10. Из трех станков, обслуживаемых одним рабочим, вероятность остановки на протяжении одного часа составляет для I станка 0,2, для II — 0,15 и для III — 0,12. Какова вероятность бесперебойной работы всех трех станков на протяжении одного часа?

Решение. Здесь бесперебойность работы станка - событие, противоположное рАбОте с остановкой. Поэтому, есЛИ данО то соответственно вероятности бесперебойной работы для отдельных станков составят:

Если работа каждого станка не зависит от работы других станков, то здесь теорема умножения дает

При решении некоторых задач на вычисление вероятностей приходится комбинировать теоремы сложения и умножения. Таковы, например, задачи, в которых рассматривается несколько однородных событий, независимых между собой по условиям испытаний.

В таких задачах могут ставиться ВОпросы: а) о вероятности появления одного события (один выигрыш у двух участников лотереи, имеющих по нескольку билетов, одна пробоина в мишени после трех выстрелов, произведенных разными стрелками и др.), двух событий без указания какого (или каких двух) именно и б) о вероятности появления хоть (или по крайней мере, или не менее) одного, двух событий.

В задачах первой группы следует исходить из того, что появление одного события из нескольких совмещается с непоявлением всех остальных и что такое совмещение имеет место для каждого из рассматриваемых событий. Например, при наличии двух событий А и В такому случаю соответствуют совмещения или , а при наличии трех событий — совмещения , или , или . Аналогично строятся комбинации, соответствующие условию наступления двух событий из нескольких.

Пример 11. Найти вероятность того, что жетон, наудачу взятый из всех трехзначных жетонов, содержит только одну цифру, кратную трем.

Решение. Условию задачи удовлетворяет жетон, у которого кратна трем либо цифра сотен, либо цифра десятков, либо цифра единиц. Обозначим появление требуемой цифры на месте сотен через А, На месте десятков — В и на месте единиц — С. Тогда событию А Благоприятствуют 3 исхода из 9, событию В — 3 исхода из 10 и событию С — 3 исхода из 10.

Поэтому a , так как 0 для цифры сотен исключается; а

В принятых обозначениях появление жетона с требуемой цифрой сотен есть сложное событие , с требуемой цифрой десятков — событие и с требуемой цифрой единиц — событие . Поэтому вероятность того, что только цифра сотен кратна трем, т. е. вероятность Того, что только цифра десятков кратна трем, т. е. вероятность того что лишь цифра единиц кратна трем, т. е. Так как условию задачи удовлетворяет любой из трех рассмотренных случаев, то возможно сложение вероятностей, что дает

В отношении задач с условием наступления двух событий из нескольких решение строится по такой же схеме, но рассматриваемые при этом сложные события представляются в виде , или , Или .

Навыки по решению таких задач можно получить самостоятельной работой над рекомендуемыми упражнениями.

В задачах второй группы целесообразно обращение к полной системе событий с использованием противоположных событий.

В самом деле, если ищется вероятность наступления хоть одного из трех независимых событий А, В П С, то это значит, что должны быть учтены и просуммированы вероятности таких совместимых событий:

1) появление какого-либо одного события (при непоявлении остальных двух): или , или , или ,

2) появление каких-либо двух событий (при непоявлении третьего): или , или , или и

3) появление всех трех событий, т. Е. АВС.

Подсчет искомой вероятности заключается в отыскании вероятностей каждого из перечисленных совместных событий и затем в сложении этих вероятностей. Однако можно не прибегать к этой громоздкой операции, если учесть, что присоединение ко всем перечисленным совместным событиям еще события , состоящего в непоявлении ни одного из событий А, В и С, приводит к полной системе событий. Но это означает, что Появление хоть одного из трех событий А, В и С и непоявление ни одного из них — Это Противоположные события.

Поэтому, обозначая искомую вероятность через Р, можно записать, что

.

Этим установлено короткое и легкое выполнимое решение поставленной задачи. В порядке самостоятельной работы учащемуся рекомендуется таким способом вычислить вероятность того, что трехзначный жетон (см. пример 11) будет содержать хоть одну четную цифру (с проверкой результата путем непосредственного подсчета вероятности суммированием).

Вопросы, аналогичные поставленным, могут встречаться и при рассмотрении событий, которые по условиям испытаний оказываются зависимыми. Такое видоизменение условий должно быть при решении задач выявлено и учтено.

Пример 12. В механизм входят две детали одинакового типа. Механизм не работает, если поставлены обе детали уменьшенного размера. Сборщик располагает всего 10 деталями, из которых 3 — меньше стандарта. Найти вероятность нормальной работы механизма, если и первая и вторая детали берутся сборщиком без проверки.

Решение. По условию задачи работе механизма благоприятствуют следующие исходы подбора:

В то же время механизм не будет работать при таком исходе подбора: событие D—I деталь нестандартная и II нестандартная.

Заметив, что все четыре перечисленные сочетания деталей составляют полную систему событий, можно установить, что наступление одного из первых трех исходов и наступление четвертого исхода — противоположные события (при первом из них механизм работает, а при втором — не работает).

Поэтому .

Здесь событие D обозначает двукратное появление деталей меньше стандарта. При этом вероятность появления первой такой детали , а вероятность появления второй такой же детали уже условная:

Отсюда вероятность двукратного появления таких деталей определяется по теореме умножения для зависимых событий.

Таким образом, искомая вероятность нормальной работы МехаНизма

Определим вероятность появления одного из двух событий А И В, когда эти два события совместимы.

Здесь следует рассмотреть все исходы, в которых раССматриваемые два события вообще появляются. Это: 1) событие , 2) событие и 3) событие АВ.

Тогда искомая вероятность . Первые два слагаемых можно преобразовать, пользуясь тем, что

и .

Это дает:

и ,

Откуда окончательно имеем

.

ЭТО — обобщенная формула сложения, которая выражает вероятность появления одного из двух событий при условии их совместимости. Ранее выведенная формула при несовместимости событий А и В является частным случаем выведЕНной здесь формулы, так как , если события А И В несовместимы.

Пример 13. Найти вероятность того, что подброшенная игральная кость упадет, показав на верхней грани четное или кратное трем число кружков.

Решение. Для применения формулы сложения вероятностей двух совместимых событий найдем:

1) вероятность появления четного числа очков (число всех граней П=6, число граней с четным количеством кружков );

2) вероятность появления числа очков, кратного трем, (число граней с кратным трем количеством кружков );

3) вероятность появления числа очков и четного, и кратного трем (число граней с таким числом очков ).

Теперь по обобщенной формуле сложения вероятностей получаем

Пусть дана система единственно возможных и несовместимых событий и событие Е, которое может наступить лишь совместно с одним из событий заданной системы. Требуется найти вероятность появления события Е, если известны вероятности и . С такой задачей связано, например, вычисление вероятности попадания на сборку стандартной детали из общей партии деталей, изготовленных на нескольких станках, если для каждого станка известны его доля в общем выпуске и процент стандартных деталей в общем числе выпускаемых деталей.

Искомая вероятность (или или , …, или ), поскольку наступление события Е только и возможно при наступлении одного из несовместных событий или и Е, или и Е, …, или и Е. По этому по теореме сложения вероятностей

.

Применяя к каждому слагаемому теорему умножения вероятностей, будем иметь

.

Отсюда

,

Или

.

Это — формула полной вероятности.

Пример 14. Пластмассовые болванки изготовляются на трех прессах. I пресс вырабатывает 50% всех болванок, II — 30% и III — 20%. При этом:

Найти вероятность того, что наудачу взятая со склада болванка соответствует стандарту.

Решение. Здесь ( — Появление болванки с I пресса, — со II пресса и — С III пресса). Если событие Е обозначает соответствие болванки стандарту, то для отдельных прессов имеем следующие условные вероятности выпуска стандартных болванок:

Отсюда

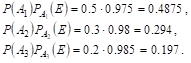
Таким образом

Т. Е. вероятность того, что взятая наудачу со склада болванка стандартна, равна 0,9785.

Если событие Е произошло, но неизвестно, совместно с каким из событий , то может возникнуть вопрос об определении вероятности того, что событие Е наступило вместе с каким-то одним событием из всех единственно возможных. При такой постановке вопроса события оказываются гипотезами, вероятности которых в последующем порядке (a posteriori) следует определить.

Произвольное слагаемое из формулы полной вероятности является произведением, симметричным относительно своих множителей, поскольку события и Е зависимы. Поэтому

.

Отсюда находим вероятность гипотезы :

Или

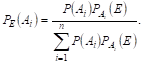
Это — формула Байеса. Для контроля правильности вычисленных вероятностей гипотез следует пользоваться условием , так как гипотезы Образуют полную систему.

Пример 15. По условию предыдущего примера вычислить вероятность того, что соответствующая стандарту болванки изготовлена а) на I, б) на II, в) на III прессе.

Решение. а) Для гипотезы , пользуясь формулой Байеса, получаем

Б) Для гипотезы по той же формуле имеем

В) Для гипотезы аналогично получаем

Правильность вычислений подтверждается тем, что

< Предыдущая		Следующая >