64. Целочисленные задачи линейного программирования. Метод Гомори

Экономическая и геометрическая интерпретация задачи целочисленного программирования. Экстремальная задача, переменные которой принимают лишь целочисленные значения, называется задачей целочисленного программирования.

В математической модели задачи целочисленного программирования как целевая функция, так и функции в системе ограничений могут быть линейными, нелинейными и смешанными. Ограничимся случаем, когда целевая функция и система ограничений задачи являются линейными.

1.20. В цехе предприятия решено установить дополнительное оборудование, для размещения которого выделено площади. На приобретение оборудования предприятие может израсходовать 10 тыс. руб., при этом оно может купить оборудование двух видов. Комплект оборудования I вида стоит 1000 руб., а II вида — 3000 руб. Приобретение одного комплекта оборудования I вида позволяет увеличить выпуск продукции в смену на 2 ед., а одного комплекта оборудования II вида — на 4 ед. Зная что для установки одного комплекта оборудования I вида требуется 2 м2 площади, а оборудования II вида — 1 м2 площади определить такой набор дополнительного оборудования, которых дает возможность максимально увеличить выпуск продукции

Решение. Составим математическую модель задачи. Предположим, что предприятие приобретет комплектов оборудования I вида и комплектов оборудования II вида. Тогда переменные и должны удовлетворять следующим неравенствам:

(8)

Если предприятие приобретет указанное количество оборудоВания, то общее увеличение выпуска продукции составит

(9)

По своему экономическому содержанию переменные и могу принимать лишь целые неотрицательные значения, т. е.

(10)

, - целые. (11)

Таким образом, приходим к следующей математической задаче: найти максимальное значение линейной функции (9) при вы полнении условий (8), (10) и (11). Так как неизвестные могут принимать только целые значения, то задача (8) - (11) является задачей целочисленного программирования. Поскольку число неизвестных задачи равно двум, решение данной задачи можно найти, используя ее геометрическую интерпретацию. Для этого прежде всего построим многоугольник решений задачи, состоящей в определении максимального значения линейной функции (9) при выполнении условий (8) и (10) (рис. 11). Координаты всех точек построенного многоугольника решений ОАЕВС Удовлетворяют системе линейных неравенств (8) и условию неотрицательности переменных (10). Вместе с тем условию (11), т. е. условию целочисленности переменных, удовлетворяют координаты лишь 12 точек, отмеченных на рис. 11. Чтобы найти точку, координаты которой определяют решение исходной задачи, заменим многоугольник ОАВС многоугольником OKEMNF, содержащим все допустимые точки с целочисленными координатами и таким, что координаты каждой из вершин являются целыми числами. Значит, если найти точку максимума функции (9) на многоугольнике OKEMNF, то координаты этой точки и определят оптимальный план задачи.

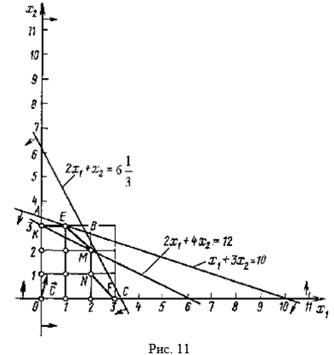
Для этого построим вектор и прямую проходящую через многоугольник решений OKEMNF (число 12 взято произвольно). Построенную прямую передвигаем в направлении вектора до тех пор, пока она не пройдет через последнюю общую точку ее с данным многоугольником. Координаты этой точки и определяют оптимальный план, а значение целевой функции в ней является максимальным.

В данном случае искомой является точка E(1; 3), в которой целевая функция принимает максимальное значение Следовательно, координаты точки Е определяют оптимальный план задачи (8) - (11). В соответствии с этим планом предприятию следует приобрести один комплект оборудования 1 вида и три комплекта оборудования II вида. Это обеспечит предприятию при имеющихся у него ограничениях на производственные площади и денежные средства максимальное увеличение выпуск продукции, равное 14 ед. в смену.

1.21. Для выполнения работ могут быть использованы П механизмов. Производительность I-го механизма при выполнении J-Й работы равна . Предполагая, что каждый механизм может быть использован только на одной работе и каждая работа может выполняться только одним механизмом, определить закрепление механизмов за работами, обеспечивающее максимальную производительность. Построить математическую модель задачи.

Решение. Введем переменную , значение которой равно 1, если при выполнении I-й работы используется J-Й механизм, и равно 0 в противном случае. Тогда условия использования каждого механизма только на одной работе выражаются равенствами

(12)

А условия выполнения работы только одним механизмом — равенствами

(13)

(14)

Таким образом, задача состоит в определении таких значений неизвестных , удовлетворяющих системам уравнений (12) и (13) и условию (14), при которых достигается максимальное значение функции

(15)

Сформулированная задача является задачей целочисленного программирования.

Определение оптимального плана задачи целочисленного программирования. Рассмотрим задачи целочисленного программирования, в которых как целевая функция, так и функции в системе ограничений являются линейными. В связи с этим сформулируем основную задачу линейного программирования, в которой переменные могут принимать только целые значения. В общем виде эту задачу можно записать так: найти максимум функции

(16)

При условиях

(17)

(18)

- целые (19)

Если найти решение задачи (16) - (19) симплексным методом, то оно может оказаться как целочисленным, так и нет (примером задачи линейного программирования, решение которой всегда является целочисленным, служит транспортная задача). В общем же случае для определения оптимального плана задачи (16) - (19) требуются специальные методы. В настоящее время существует несколько таких методов, из которых наиболее известным является метод Гомори, в основе которого лежит описанный выше симплексный метод.

Метод Гомори. Нахождение решения задачи целочисленного программирования методом Гомори начинают с определения симплексным методом оптимального плана задачи (16) - (18) без учета целочисленности переменных. После того как этот план найден, просматривают его компоненты. Если среди компонент нет дробных чисел, то найденный план является оптимальным планом задачи целочисленного программирования (16) - (19). Если же в оптимальном плане задачи (16) - (18) переменная принимает дробное значение, то к системе уравнений (17) добавляют неравенство

(20)

И находят решение задачи (16) - (18), (20).

В неравенстве (20) и — преобразованные исходные величины и значения которых взяты из последней симплекс-таблицы, а и — дробные части чисел (под дробной частью некоторого числа а понимается наименьшее неотрицательное число B такое, что разность между А и B есть целое). Если в оптимальном плане задачи (16) - (18) дробные значения принимают несколько переменных, то дополнительное неравенство (20) определяется наибольшей дробной частью.

Если в найденном плане задачи (16) - (18), (20) переменные принимают дробные значения, то снова добавляют одно дополнительное ограничение и процесс вычислений повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования (16) - (19), либо устанавливают ее неразрешимость.

Если требование целочисленности (19) относится лишь к некоторым переменным, то такие задачи называются Частично целочисленными. Их решение также находят последовательным решением задач, каждая из которых получается из предыдущей с помощью введения дополнительного ограничения. В этом случае такое ограничение имеет вид

(21)

Где определяются из следующих соотношений:

1) для , которые могут принимать нецелочисленные значения,

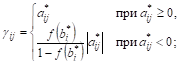(22)

2) для , которые могут принимать только целочисленные значения,

(23)

Из изложенного выше следует, что процесс определения оптимального плана задачи целочисленного программирования методом Гомори включает следующие основные этапы:

1. Используя симплексный метод, находят решение задачи (16) - (18) без учета требования целочисленности переменных.

2. Составляют дополнительное ограничение для переменной, которая в оптимальном плане задачи (16) - (18) имеет максимальное дробное значение, а в оптимальном плане задачи (16) - (19) должна быть целочисленной.

3. Используя двойственный симплекс-метод, находят решение задачи, получающейся из задачи (16) - (18) в результате присоединения дополнительного ограничения.

4. В случае необходимости составляют еще одно дополнительное ограничение и продолжают итерационный процесс до получения оптимального плана задачи (16) - (19) или установления ее неразрешимости.

1.22. Методом Гомори найти максимальное значение функции

(24)

При условии

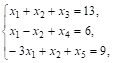(25)

(26)

- целые (27)

Дать геометрическую интерпретацию решения задачи.

Решение. Для определения оптимального плана задачи (24) - (27) сначала находим оптимальный план задачи (24) - (26) (табл. 22).

Как видно из табл. 22, найденный оптимальный план задачи (24) - (26) не является оптимальным планом задачи (24) - (27), поскольку две компоненты и имеют нецелочисленные значения. При этом дробные части этих чисел равны между собой. Поэтому для одной из этих переменных составляется дополнительное ограничение. Составим, например, такое ограничение для переменной . Из последней симплекс-таблицы (табл. 22) имеем

Таким образом, к системе ограничений задачи (24) - (27) добавляем неравенство

или

Т. е.

(28)

Находим теперь максимальное значение функции (24) при выполнении условий (25), (26) и (28) (табл. 23).

Из таблицы 23 видно, что исходная задача целочисленного программирования имеет оптимальный план При этом плане значение целевой функции равно . Дадим геометрическую интерпретацию решения задачи. Областью допустимых решений задачи (24) - (26) является многоугольник OABCD (рис. 12). Из рис. 12 видно, что максимальное значение целевая функция принимает в точке С (19/2; 7/2), т. e. что Х = (19/2; 7/2; 0; 0; 34) является оптимальным планом. Это непосредственно видно и из таблицы 22. Так как Х = (19/2; 7/2; 0; 0; 34) не является оптимальным планом задачи (24) - (27) (числа и - дробные), то вводится дополнительное ограничение . Исключая из него и подстановкой вместо них соответствующих значений из уравнений системы ограничений (25), получим отсекающий от многоугольника OABCD треугольник EFC.

Как видно из рис. 12, областью допустимых решений полученной задачи является многоугольник OABEFD. В точке Е(9; 4) этого многоугольника целевая функция данной задачи принимает максимальное значение. Так как координаты точки Е – целые числа и неизвестные , и принимают целочисленные значения при подстановке в уравнение (25) значений и , то является оптимальным планом задачи (24) - (27). Это следует и из таблицы 23.

2.5. Методом Гомори найти решение задачи, состоящей в определении максимального значения функции

(29)

При условиях

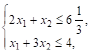(30)

(31)

- целые. (32)

Дать геометрическую интерпретацию решения задачи.

Решение. Сформулированную задачу перепишем так: найти максимальное значение функции

(33)

При условиях

(34)

(35)

- целые. (36)

Задача (33) – (36) является частично целочисленной, так как переменные и могут принимать нецелочисленные значения.

Находим симплексным методом решение задаяи (33) – (35) (таблица 24).

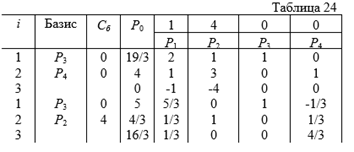
После II итерации получаем оптимальный план данной задачи При этом плане переменная приняла нецелочисленное значение. Поэтому необходимо перейти к новой задаче, добавив к системе ограничений (33) – (35) еще одно ограничение или

(37)

Находим теперь решение задачи, состоящей в определении максимального значения функции (33) при условиях (34), (35) и (37). Данную задачу решаем двойственным симплекс-методом (таблица 25).

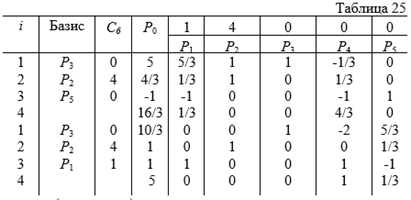
Из таблицы 25 видно, что является оптимальным планом построенной задачи. Так как при этом плане переменные и принимают целые значения, то он также является оптимальным планом исходной задачи (33) – (36).

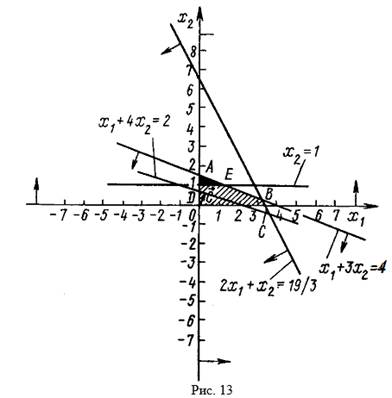
Дадим геометрическую интерпретацию решения задачи. На рис. 13 показана область допустимых решений задачи (33) – (35). Из рисунка видно, что максимальное значение целевая функция принимает в точке , т. е. что является оптимальным планом задачи (33) – (35). В то же время не является планом задачи (33) – (36), так как переменная принимает дробное значение. Поэтому вводим дополнительное ограничение откуда, подставляя вместо его значение из второго уравнения системы уравнений (34), получаем . Этому неравенству на рис. 13 соответствует полуплоскость, ограниченная прямой , отсекающей от многоугольника ОАВС треугольник ADE. В области ODEBC находим точку Е(1; 1), в которой функция (33) принимает максимальное значение. Так как координаты точки Е — целые числа, то является оптимальным планом задачи (33) - (37). Это видно и из таблицы 25.

< Предыдущая		Следующая >