42. Перестановки с повторениями
Четыре цифры 1, 2, 3, 4 можно переставлять друг с другом ![]() способами. В слове «мама» четыре буквы. Но перестановок из этих букв можно составить не 24, а только 6:
способами. В слове «мама» четыре буквы. Но перестановок из этих букв можно составить не 24, а только 6:
МамА, Маам, Ммаа, Амам, Аамм, Амма.
Чтобы поНЯть, почему так случилось, поставим в сООтветствие цифрам 1 и 2 букву «м», а цифрам 3 и 4 — букву «а». Тогда, например, перестановке 1234 будет соответствовать слово Ммаа, а перестановке 1324 — слово мама. Но слово ммаа соответствует не только перестановке 1234, но и еще трем перестановкам: 2134, 1243 и 2143. Читатель может убедиться в этом прямой подстановкой букв вместо цифр. Но более поучительно такое рассуждение: если цифры 1 и 2 меняются местами, то в соответствующем слове меняются меСТами две буквы «м», а потому само слово остается неизменным. Неизменным оно оСТается и при взаимной переСТановке цифр 3 и 4, — при этом в слове меняются местами две буквы «а». Теперь Ясно, как из любой перестановки получить перестановки, прИВодящие к тому же самому слову: можно либо оставИТь ЭТу перестановку неизменной, либо поменять в ней местами цифры 1 и 2, либо поменять местами цифры 3 и 4, лИБо, наконец, одновременно переставить 1 и 2, а также 3 и 4. Всего получается 4 перестановки цифр, отвечающие одному и тому же слову. Отсюда видно, что все множество из 24 перестановок цИФр 1, 2, 3, 4 распадается на четверки, дающие одно и то же слово. Поэтому число различных слов равно 4!/4 = 6. Вот эти четверки перестановок:
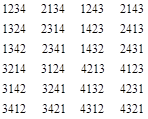
Рассмотрим теперь задачу в общем виде. Пусть Дан Кортеж длины П, составленный из элементов множества ![]() , причем буква
, причем буква ![]() входит в ЭТот кортеж
входит в ЭТот кортеж ![]() раз,..., буква
раз,..., буква ![]() —
— ![]() раз. Тогда
раз. Тогда ![]() . Если переставлять в этом кортеже буквы, будут получаться новые кортежи, имеющие тот же состав, т. Е. Такие, что буква
. Если переставлять в этом кортеже буквы, будут получаться новые кортежи, имеющие тот же состав, т. Е. Такие, что буква ![]() входит в них
входит в них ![]() раз,..., буква
раз,..., буква ![]() Входит
Входит ![]() раз. Мы будем называть эти кортежи ПеРесТАНовками с повторениями из букв
раз. Мы будем называть эти кортежи ПеРесТАНовками с повторениями из букв ![]() , имеющими состав
, имеющими состав ![]() . Число таких перестановок Обозначим
. Число таких перестановок Обозначим ![]() .
.
С помощью правила произведения находим, что число перемещений букв, не меняющих данную перестановку, равНО ![]() Но П чисел можно переставлять друг с другом П! способами. Поэтому число различных перестановок букв, имеющих состав
Но П чисел можно переставлять друг с другом П! способами. Поэтому число различных перестановок букв, имеющих состав ![]() , т. е.
, т. е. ![]() , в
, в ![]() раз меньше, чем П!:
раз меньше, чем П!:
![]() , (5)
, (5)
Пользуясь формулой (5), легко узнать, например, сколько различных кортежей получится, если переставлять буквы слова «математика». Это слово имеет состав (2, 3, 2, 1, 1, 1) и потому получается
![]()
Кортежей.
| < Предыдущая | Следующая > |
|---|