29. Графическое решение

Теорема, которую мы сЕЙчас доказали, относится к разряду так называЕмЫх «теорем существования», утверЖдАющих, что НЕчто (в нашем случае — подбор невест) существует, но дающих мало информации о том, как это нечто найти (в нашем случае — как конкретно организовать свадьбы или выбор ПРедставителей). Ведь ЕСли буквально Следовать доказательству теоремы, то надо сначала перебрать все подмножества в множестве юношей и посмотреть, нет ли среди них критических. А в следующей главе будет доказано, что число подмножеств в мНОжестве из П Элементов равНО , так что уже при 20 юношах число подмноЖЕств будет больше миллиона и ПРидется приГнУть к услугам электронНОй свахи.

А если учесть, что с подобными задачами приходится иметь дело в куда более серЬЕзных вопросах, чем ДеревенскиЕ сВАдьбы (наПРимер, при распределении работ между БАНКами, оргаНИзации транспортных потоков и т. Д.), То стаНОвИТся ясНО, Насколько желателен алгоритм, Позволяющий осуществлять выбор представителей, а в случае, когда он невозможен, указывающий наИБольшее Число возМОжных выборов (НАпример, устройство максимальНогO чисЛА свадеб). Один из путей решЕНия осНОван на использовании Графов — мНОжеств, состоящих из конечного числа точек, НеКоторые пары которых соединены дугами (такие графы НазывАЮтсЯ НеориентироВАнными; если вместо дуг РисоВать стрЕЛкИ, то получится Ориентированный граф, или, КОроче, Орграф). Начертим такой граф: в одНОм столбце посТаВИм точки, ИЗображающие подмножества , а во втором — точки, изображающие элемеНТы всего множества X. Каждую точку, изображаЮЩую подмножество, соЕДИниМ дугами со всеми входящими в НеГо элементами. НАпример, распределение друзей, о котором говорилось в предыдущем пункте, изображено НА рис. 6.

Предположим, что мы каким-то образом НАзначили представителей некоторых подМНожеств, т. е. выбрали некоторые дуги нашего графа. Пометим эти дуги знаком «плюс». Разумеется, две Помеченные дуги не могут иметь общих

Концов, иначе мы лИБо выбрали бы в одНОм МноЖестве двух представителей, лИБо один элемЕНт представлял Бы Два разНЫх множества. Если в результате оказалось, чТО ИЗ каждого подмножества выходит помеченная дуга, то все в порядке — все подмножества получали представителей. В противном случае берем все подмножества, лишенные представительства, и помечаем их цифрой 1. Все элементы, к которым идут дуги из помеченных ЦиФрОй 1 подмножеств, отметим цифрой 2. Если хотя бы оДин Из Этих элементов свободен, т. Е. не является ничьим представителем, то назНАчаем его представителем того Подмножества, от которого к нему шла дуга и тем самыМ увеличим число представленных подмножеств.

Сложнее обстоит дело, если среди помеченных цифрой 2 элементов нет свободных, — все они уже Кого-нибудь Представляют. В этом случае придется менять ранее Принятые решения и делать перестройку, высвобождая эти элементы. Заметим, что при таком предположенИИ всЕ элементы, помеченные цифрой 2, являются концами дуг с пометкой плюс, и мы можем по таким дугам верНУтьСя От этих элементов в столбец подмножеств. Подмножества, к которым мы вернемся, пометим цифрой 3, а все элементы, к которым ИДут не отмеченные знаком «плюс» дуги из помеченных цифрой 3 подмножеств, отметим цифроЙ 4. Дальше по отмеченным знаком «плюс» дугам вернемся в столбец подмножеств, и пометим их цифрой 5, а затем по всем неотмеченным дугам, начинающимся в Подмножествах с пометкой 5, переймем к элементам множества, и пометим их цифрой 6 (при этом одно и то же подмножество, или один и тот же элемент, может иметь несколько помеТок). Будем продолжать описаНнЫЙ выше процесс до тех пор, пока в столбце элементов мы не наткнемся на СвоБодный элемент. Тогда у нас получится «молния», начинающаяся с подмножества, помеченного цифрой 1 (т. е. еще НE имеющего представителя) и коНЧающаяся свободНыМ элемеНТом (рис. 7).

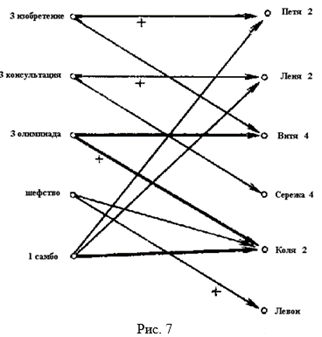
Дуги Этой «молнии» через одНУ Помечены знаками «плюс». А теперь изменим пометкИ этих дуг — все непомечеННые дуги молнии пометим знаком «плюс», и сотрем все бывшие ранее на ней знаки «плюс». НЕТрудно видеть, что в результате этой операции число представленных подмНОжеств увеличилось на единицу, — оказалось представленным подмножество, с которого начИНается молнИЯ. Если и теперь не все подмножества имеют представителей, то повторим этот процесс. В конце коНЦов произойдет одно из двух: либо все подмножества получат представителей, либо после одного из циклов пометок число помеченных элементов НЕ увеличится. Во втором случае задача о различных представителях оказывается НЕразрешимой, и мы лишь получаем наибольшее число представленных подмножеств. Разумеется, если выполнено условие теоремы о различных представителях, то второй случай невозможеН.

ОтмЕТим изящное достаточное условие разрешимости задачи о назначении представителей.

Если существует такое число K, что каждое Noдмножество из числа Содержит ровно K Элементов, А каждый элемент из множества Х принадлежит ровНо K подмножествам, то можно наЗНачить различных ПредстаВителей.

< Предыдущая		Следующая >