05. Полугруппы, группы, структуры

Полугруппы. Полугруппой называется алгебра с одной ассоциативНОй бинарной операцией. Эта операция обычно называется умножением, поэтому результат ее применения к элементам A и B записывается как или АB. Такая запись называется мультипликативной. В частности, Аа принято записывать как , Ааа как А3 и т. д. В общем случае Если же умножение коммутативно, то полугруппа называется коммутативной, или Абелевой. Если полугруппа содержит такой элемент Е, Что для любого А Aе = Еа = А, то Е называется Единицей. Полугруппа с единицей называется Моноидом. Единица в полугруппе всегда единственна. Действительно, если есть две единицы и , то и ; следовательно,

Композиция отображений является ассоциативной операцией. Поэтому всякое множество преобразований (отображений некоторого множества в себя), замкнутое относительно композиции, является полугруппой. Рассмотрим пример. Пусть на множестве {1,2,3} заданы преобразования

и

Их произведения имеют вид

и

Т. е. не совпадают С A и B. Поэтому множество не замкнуто относительно композиции и не образует полугруппы. Однако если к нему добавить преобразования и , то можно убедиться, что полученное множество вместе с операцией композиции образует полугруппу. ТАблица Кэли этой полугруппы имеет вид:

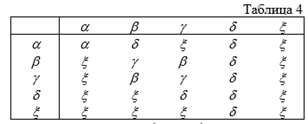
Если же к Г добавить тождественное отображение ПолУЧим полугруппу с единицей.

Теорема 1. Любая полугруппа с единицей изоморфна некотОРой полугруппе преобразований.

Действительно, пусть задана полугруппа с множеством . Каждому элементу полугруппы поставим в соответствие преобразование множества М следующим образом: Для всех Тогда произведению будет соответствовать преобразование т. е. композиция преобразований и ; следовательно, условие (1) гомоморфизма выполнеНО. Кроме того, разным элементАМ М соответствуют разные отображения, так как и, следовательно, Таким образом, соответствие является изоморфизмом. 

Если любой элемент полугруппы можно представить как произведение некоторого числа элементов множества то множество называется порождающим множеством или Системой образующих полугруппы Р, а его элементы называются Образующими. В нашем примере образующими являются A и B, так как . В полугруппе порождающим множеством служит бесконечное множество простых чисел. Если полугруппа имеет только одну образующую, то все элементы являются степЕНями этой образующей. Такая полугруппа называется Циклической. Циклической полугруппой является, например, полугруппа , так как все натуральные числа — это суммы некоторого количества единиц. Пусть полугруппа Р имеет конечное множество образующих . Если обознАЧения операции опустить (как это обычно делается для умножения), то все элементы Р можно рассматривать как слова в алфавите . Некоторые различные слова могут оказаться равными как элементы. В нашем примере полугруппы преобразований выполняются, например, равенства В коммутативной полугруппе для любых элементов А, B выполняются равенства АB = Bа. Такие равенства называются Определяющими соотношениями. Если же в полугруппе нет определяющих соотношений, т. е. любые два различных слова являются различными элементами полугруппы, то полугруппа называется Свободной.

Всякую полугруппу можно получить из свободной полугруппы вВЕдением некоторых определяющих соотНОшений. Элементы заданной так полугруппы — это слова в алфавите образующих, причем некоторые слова равны (т, е. задают один и тот же элемент) в силу определяющих соотношений. Отношение равенства слов является отношением эквивалентности. Из любого слова, используя определяющие соотношения, легко можно получить различные эквивалентные ему слова. Намного сложнее проблема: для двух данных слов выяснить, можно ли получить одно из другого, используя определяющие соотношения.

Группы. Группой называется полугруппа с единицей, в которой для каждого элемента А существует элемент , называемый Обратным К А и удовлетворяющий условию Число элементов группы называется порядком группы. Группа, в которой операция коммутативна, называется коммутативной, или абелевой. Группа, все элементы которой являются степенями одного элемента А, НазыВается циклической. Циклическая группа всегда Абелева. Для Абелевых групп часто употребляется аддитивная запись: операция обозначается как сложение, а единица обозначается 0.

Пример 3.

1) Множество рациональных чисел, не содержащее нуля, с операцией умножения является абелевой группой. Обратным к элементу А является элемент

2) Множество целых чисел с операцией сложения является абелевой циклической группой. Роль единицы здесь играет 0, обратным к элементу А является элемент — А.

3) Множество невырожденных квадратных матриц порядка П. (с отличным от 0 определителем) с операцией умножения является некоммутативной группой.

4) Множество {0, 1, 2, 3, 4} с операцией «сложение по mod 5» — конечная абелева циклическая группа. В этой группе

5) Алгебра , где О — множество поворотов квадрата, а — их композиция, является циклической группой: Единицей в ней служит тождественное отображение A (поворот на нулевой угол); обратным к данному повороту служит поворот, дополняющий его до

6) Рассмотрим множество S всех взаимно-однозначных преобразований конечного множества М в себя. Такие преобразования называются подстановками. Алгебра представляет собой группу, которая называется Симметрической. Поскольку число подстановок равно числу перестановок в списке элементов М, то порядок РавеН Симметрическая группа не является Абелевой. Пусть, например, Тогда В любой конечной группе ее операция (умножение) может быть задана таблицей КэЛи. Для групп таблица Кэли имеет важную особенность: любой ее столбец содержит все элементы группы. Действительно, если столбец не содержит какого-нибудь элемента, то некоторый другой элемент в нем должен встретиться дважды, скажем, в K-й и L-й Строках. Но тогда и, следовательно, Умножая обе части равенства на , получаем что неверно. Таким образом, I-й столбец таблицы Кэли, т, Е. умножение на является подстановкой на множестве элементов группы. Проверив, что это соответствие является изоморфизмом (аналогичную проверку мы делали для полугрупп преобразований), получаем теорему Кэли.

Теорема 2. Любая конечная группа изоморфна группе ПодстаНовок на множестве ее элементов. 

Из сравнения теорем о связи полугрупп с преобразованиями и групп с подстановками видно, что группа — это полугруппа взаимнооднозначных преобразований, причем именно взаимная однозначность гарантирует наличие обратного преобразования. Можно сказать, Что В группе при любом числе умножений не теряется информация об исходном элеменТЕ: если известно, на что умножали, всегда можно узнать, что умножали. Для полугруппы это верно не всегда. Используя термиНОлогию дискретных систем, то же самое можно сказать следующим образом. Пусть имеется дискретная система с конечным числом состояний , на вход которой может быть подано входное воздействие из множества Всякое входное воздействие однозначно переводит состояние системы в некоторое другое состояние и, следовательно, является преобразованием множества S. Последовательности воздействий — это композиции преобразований; следовательно, множество всех последовательностей является полугруппоЙ С образующими . Если такая полугруппа оказывается группой, то это означает, что по любой входной последовательности и заключительному состоянию системы можно однозначно определить начальное состояние системы.

Алгебраические системы. Структуры. До сих пор рассматривались алгебры, т. е. множества, на которых заданы операции. Множества, на которых кроме операций заданы отношения, называются Алгебраическими системами. Таким образом, алгебры можно считать частным случаем алгебраических систем (в которых мНОжество отношений пусто). Другим частным случаем алгебраических систем являются Модели — множества, на которых заданы только отношения. Понятие изоморфизма для алгебраических систем вводится аналогично тому, как это было сделано ранее для алгебр, с той разницей, что к условию (1) сохранения операций добавляется условие сохранения отношениЙ При изоморфизме.

Рассмотрим здесь лишь один пример алгебраической системы, который наиболее часто встречается в теоретической алгебре и ее применениях. Этот пример — структура.

Пусть задано частично упорядоченное множество М. Отношение порядка в дальнейшем будем обозначать £. Для элементов А и B из М Их верхней гранью называется любой элемент , такой, что а их нижней гранью — любой элемент такой, что В общем случае для некоторых элементов А и B верхняя или нижняя грань может не существовать или быть неединственной, причем различные верхние (или нижние) грани могут быть несравнимыми.

Структурой называется частично упорядоченное множество, в котором для любых двух элементов А и B существует их ПересечениЕ — такая нижняя грань А и B, что любая другая нижняя грань А и B меньше С; их Объединение — такая верхняя грань А и B, что любая другая верхняя грань А и B больше D. Таким образом, структура — это алгебраическая система С одним бинарным отношением и двумя бинарными операциями.

Пересечение и объединение ассоциативны (предлагаем читателю это доказать!), поэтому можно говорить о пересечении и объединении любого конечного Подножества элементов структуры.

Пример 4.

1) Любое полностью упорядоченное множество М (например, множество целых чисел) можно превратить в структуру, определив для любых

2) Определим на N отношение частичного порядка следующим образом: , если А делит B. Тогда — наименьшее общее кратное А и B, — наибольший общий делитель А, B. Например,

3) Система всех подмножеств любого множества А Частично упорядочена по включению: если и только если Эта система является структурой, элементами которой являются множества, а операциями — обычные Теоретико-множественные операции объединения и пересечения.

4) Рассмотрим множество двоичных векторов длины П, частично упорядоченное так, как эТО сделано в примере 1.14, П. 1.3. Для двоичных векторов это упорядочение выглядит так: если в векторе W единицы стоят на всех тех местах, на которых они стоят в N (и, быть может, еще на некоторых). Например, а и не сравнимы. МножестВО , упорядоченное Таким образом, является структурой; в ней — это вектор, в котором единицы стоят на тех (и только тех) местах, где есть единицы либо в N, либо в W, А — это вектор, в Котором единицы стоят на тех и только тех местах, где единицы есть и в N, и в W. Например, При ДОказательстве теоремы 2 п. 1.2 было установлено взаимно-однозначное соответствие между множеством и системой всех подмножеств любого Множества А мощности N. Легко проверить, что это соответствие является изоМОрфизмом соответствующих структур; таким образом, структура, описанная в примере 4 и структура из настоящего примера изоморфны.

Конечное упорядоченное множество можно изобразить диаграммой, в которой элементам соответствуют точки; из точки А ведет стрелка в точку B, если А < B и нет такого С, что А < С < B. Например, структура изображается диаграммой на рис. 2, А.

На языке диаграмм хорошо иллюстрируются все основные понятия, связанные со структурами: , если и только если существует путь из стрелок, ведущий из A в B, верхняя грань A и B — это элемент, в который есть путь из А и из B, нижняя грань А И B — это элемент, из которого есть путь и в А, и в B.

Когда упорядоченное множество не является структурой? В двух случаях: 1) когда какие-либо два элемента не имеют верхней или нижней грани (на рис. 2, Б элементы D и Е, с и D не имеют верхней грани, элементы B и С не имеют нижней грани); 2) когда для некоторой пары элементов наименьшая верхняя (или наибольшая, нижняя) грань не единственна (на рис. 2, В все элементы имеют верхние и нижние грани, однако B и С имеют две наименьшие и несравнимые верхние грани, D и Е имеют две наибольшие нижние грани, поэтому изображенное на этом рисунке множество не является структурой).

Конкретный пример первого случая можно получить из структуры удалением некоторых ее элементов. Из рис. 2, А видно, что после удаления 101 остается структурой, а после удаления 111 — нет. Удалением элементов из структуры можно получить и пример второго случая: если в удалить все элементы, кроме 0000, 0010, 0100, 0111, 1110, 1111, то диаграмма для оставшихся элементов в точности совпадет с рис. 2, В.

Структура, в которой пересечение и объединение существуют Для Любого подмножества ее элементов, называется Полной. Ввиду отмеченной ранее ассоциативности пересечения и объединения конечная стрУКтура всегда полна. Объединение всех элементов полной структуры — это максимальный элемент структуры, называемый Единицей структуры. Пересечение всех элементов полной структуры — это минимальный элемент структуры, называемый Нулем структуры. Структура из прИМера 4 п. 3 всегда полна (в том числе и для бесконечного А). Единицей этой структуры служит само множество (содержащее любое Свое Подмножество), нулем — пустое множество.

< Предыдущая		Следующая >