11. Отыскание начального опорного плана путем преобразования таблицы Жордана
Для заполнения таблицы Жордана каноническую форму ЗЛП преобразовываем к следующему виду:
![]() (2.11)
(2.11)
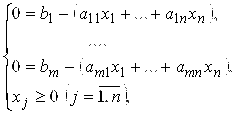 (2.12)
(2.12)
Где все ![]() .
.
Таблица Жордана содержит ![]() столбцов, где
столбцов, где ![]() – число переменных,
– число переменных, ![]() – число переменных в предпочтительном виде и
– число переменных в предпочтительном виде и ![]() строк, где
строк, где ![]() – число ограничений-равенств. В столбце «БП» записываются базисные (предпочтительные) переменные. Если ограничение не имеет предпочтительной переменной, то записывается 0. Столбец «1» – столбец свободных членов
– число ограничений-равенств. В столбце «БП» записываются базисные (предпочтительные) переменные. Если ограничение не имеет предпочтительной переменной, то записывается 0. Столбец «1» – столбец свободных членов ![]()
![]() системы ограничений (2.12) а в
системы ограничений (2.12) а в ![]() -строке – элемент
-строке – элемент ![]() из (2.11). Остальные столбцы «СП», в основной части которых находится элементы
из (2.11). Остальные столбцы «СП», в основной части которых находится элементы ![]() из системы (2.12). В
из системы (2.12). В ![]() -строке, в столбцах «СП», записываются коэффициенты при свободных переменных, стоящие в скобках выражения (2.11). Каждому ограничению-равенству из системы (2.12) соответствует строка основной части таблицы. Целевой функции (2.11) соответствует последняя строка таблицы (таблица 4).
-строке, в столбцах «СП», записываются коэффициенты при свободных переменных, стоящие в скобках выражения (2.11). Каждому ограничению-равенству из системы (2.12) соответствует строка основной части таблицы. Целевой функции (2.11) соответствует последняя строка таблицы (таблица 4).
Таблица 4
|
СП | ||||||
|
БП |
1 |
|
… |
|
... |
|
|
0 |
|
|
… |
|
... |
|
|
... |
... |
... |
… |
... |
.... |
... |
|
0 |
|
|
… |
|
... |
|
|
... |
... |
... |
… |
... |
... |
... |
|
0 |
|
|
… |
|
... |
|
|
|
|
|
… |
|
... |
|
Для нахождения начального опорного плана необходимо в результате Жордановых преобразований избавиться от нулей в первом столбце таблицы.
Преобразование таблицы называется шагом Жордановых исключений и осуществляется относительно выбранного разрешающего элемента. Разрешающий элемент выбирается среди положительных чисел основной части таблицы (которая выделена ) по наименьшему отношению свободных членов (элементы столбца 1) к соответствующим Положительным элементам столбца, выбранного разрешающим.
Пусть s-ый столбец будет разрешающим, тогда если  для
для ![]() , то
, то ![]() – разрешающий элемент.
– разрешающий элемент.
Шаг Жордановых исключений осуществляется по следующим правилам:
1 Ноль первого столбца в строке разрешающего элемента меняется местами с переменной ![]() .
.
2 Разрешающий элемент заменяется обратной величиной.
3 Остальные элементы разрешающей строки делятся на разрешающий элемент.
4 Остальные элементы разрешающего столбца делятся на разрешающий элемент и меняют знак на противоположный.
5 Прочие элементы вычисляются по формуле
![]()
![]() .
.
Или диагональ прямоугольника, на которой расположен разрешающий элемент ![]() и преобразуемый элемент
и преобразуемый элемент ![]() , назовем главной, а другую диагональ – побочной. Тогда преобразованный элемент
, назовем главной, а другую диагональ – побочной. Тогда преобразованный элемент ![]() равен разности произведений элементов, расположенных на главной и побочной диагоналях, деленной на разрешающий элемент.
равен разности произведений элементов, расположенных на главной и побочной диагоналях, деленной на разрешающий элемент.
6 0-столбцы вычеркиваются.
Если система ограничений совместна, то через некоторое число шагов все нули в левом столбце будут замещены переменными ![]() . Тогда начальный опорный план найдем, приравняв свободные переменные к нулю, а базисные (столбец «БП») – к соответствующим свободным членам (столбец 1).
. Тогда начальный опорный план найдем, приравняв свободные переменные к нулю, а базисные (столбец «БП») – к соответствующим свободным членам (столбец 1).
Если в ходе Жордановых преобразований встретится 0-строка, в которой все элементы неположительные, то данная система не имеет неотрицательных решений, хотя и является совместной.
Допустим, после некоторого числа шагов Жордановых преобразований все нули в левом столбце замещены переменными ![]() , т. е. получили таблицу 5.
, т. е. получили таблицу 5.
Таблица 5
|
СП | ||||||
|
БП |
1 |
|
… |
|
... |
|
|
|
|
|
… |
|
... |
|
|
... |
... |
... |
… |
... |
... |
... |
|
|
|
|
… |
|
... |
|
|
... |
... |
... |
… |
... |
... |
... |
|
|
|
|
… |
|
... |
|
|
|
|
|
… |
|
... |
|
Тогда компоненты начального опорного плана ![]() Будут
Будут
БП: ![]() ,…,
,…, ![]() ,…,
,…, ![]() ,
,
СП: ![]() .
.
Таким образом, начальный опорный план 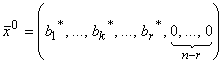 и значение целевой функции на этом плане
и значение целевой функции на этом плане ![]() .
.
Например, найдем начальный опорный план ЗЛП примера 2-м методом Жордановых исключений. Представим каноническую запись (см. пример 5) в виде (2.11)-(2.12), т. е.
![]() ;
;

Здесь в третьем и четвертом ограничениях предпочтительные переменные ![]() и
и ![]() оставлены в левой части.
оставлены в левой части.
Заполним первую Жорданову таблицу (таблица 6).
Таблица 6
|
СП |
| |||||
|
БП |
1 |
|
|
|
|
Отношения |
|
0= |
31 |
5 |
0 |
4 |
0 |
31/5 |
|
0= |
36 |
0 |
3 |
0 |
6 | |
|
|
10 |
1 |
1 |
0 |
0 |
10/1 |
|
|
10 |
0 |
0 |
1 |
1 | |
|
|
0 |
–8 |
–7 |
–4 |
–2 |
Начальный опорный план будет найден, если в первом столбце таблицы все нули в ходе преобразований Жордана будут заменены переменными ![]() .
.
Пусть ![]() -столбец будет разрешающим. Для нахождения разрешающей строки составим отношения свободных членов к соответствующим положительным элементам этого столбца. Так как в этом столбце только два положительных элемента 5 и 1, то отношения будут
-столбец будет разрешающим. Для нахождения разрешающей строки составим отношения свободных членов к соответствующим положительным элементам этого столбца. Так как в этом столбце только два положительных элемента 5 и 1, то отношения будут ![]() и
и ![]() . Так как
. Так как ![]() , то элемент «5» и будет разрешающим. Шаг Жордановых исключений относительно найденного разрешающего элемента переводит таблицу 6 в таблицу 7.
, то элемент «5» и будет разрешающим. Шаг Жордановых исключений относительно найденного разрешающего элемента переводит таблицу 6 в таблицу 7.
Таблица 7
|
СП |
| ||||
|
БП |
1 |
0 |
X12 |
X21 |
X22 |
|
X11= |
31/5 |
1/5 |
0/5 |
4/5 |
0/5 |
|
0= |
(36´5–31´0)/5 |
0 |
(3´5–0´0)/5 |
(0´5–4´0)/5 |
(6´5–0´0)/5 |
|
X3= |
(10´5–31´1)/5 |
–1/5 |
(1´5–0´1)/5 |
(0´5–4´1)/5 |
(0´5–0´1)/5 |
|
X4= |
(10´5–31´0)/5 |
0 |
(0´5–0´0)/5 |
(1´5–4´0)/5 |
(1´5–0´0)/5 |
|
Z |
(0´5–31´(–8))/5 |
8/5 |
(–7´5–0´(–8)/5 |
(–4´5–(4´(–8)) /5 |
(–2´5–0´(–8))/5 |
Вычеркивая 0-столбец, получим таблицу 8.
Таблица 8
|
СП | ||||
|
БП |
1 |
X12 |
X21 |
X22 |
|
X11= |
6,2 |
0 |
0,8 |
0 |
|
0= |
36 |
3 |
0 |
6 |
|
X3= |
3,8 |
1 |
–0,8 |
0 |
|
X4= |
10 |
0 |
1 |
1 |
|
Z |
49,6 |
–7 |
2,4 |
–2 |
Пусть теперь разрешающим будет х22-столбец. Найдем отношения свободных членов к соответствующим положительным элементам этого столбца – ![]() и
и ![]() (таблица 9).
(таблица 9).
Таблица 9
|
СП | |||||
|
БП |
1 |
|
|
|
Отношения |
|
|
6,2 |
0 |
0,8 |
0 | |
|
0= |
36 |
3 |
0 |
6 |
36/6 |
|
|
3,8 |
1 |
–0,8 |
0 | |
|
|
10 |
0 |
1 |
1 |
10/1 |
|
|
49,6 |
–7 |
2,4 |
–2 |
Так как ![]() , то вторая строка будет разрешающей. Итак, следующий разрешающий элемент будет «6», и шаг Жордановых исключений переводит таблицу 9 в таблицу 10.
, то вторая строка будет разрешающей. Итак, следующий разрешающий элемент будет «6», и шаг Жордановых исключений переводит таблицу 9 в таблицу 10.
Таблица 10
|
СП | ||||
|
БП |
1 |
X12 |
X21 |
0 |
|
X11= |
6,2 |
0 |
0,8 |
0 |
|
X22= |
6 |
0,5 |
0 |
1/6 |
|
X3= |
3,8 |
1 |
–0,8 |
0 |
|
X4= |
4 |
–0,5 |
1 |
–1/6 |
|
Z |
61,6 |
–6 |
2,4 |
2/6 |
Вычеркивая 0-столбец, получим таблицу 11.
Таблица 11
|
СП | |||
|
БП |
1 |
X12 |
X21 |
|
X11= |
6,2 |
0 |
0,8 |
|
X22= |
6 |
0,5 |
0 |
|
X3= |
3,8 |
1 |
–0,8 |
|
X4= |
4 |
–0,5 |
1 |
|
Z |
61,6 |
–6 |
2,4 |
Найдем начальный опорный план, приравняв свободные переменные к нулю, т. е. ![]() , а базисные переменные к свободным членам, т. е.
, а базисные переменные к свободным членам, т. е. ![]() .
.
Значит, начальный опорный план: ![]() . На этом плане целевая функция:
. На этом плане целевая функция: ![]() .
.
Итак, благодаря преобразованиям Жордана, исходную задачу мы можем записать (исходя из последней таблицы) в виде
![]() ;
;

| < Предыдущая | Следующая > |
|---|