09. Отыскание начального опорного плана (1-ый пункт алгоритма)

Пусть система ограничений ЗЛП представлена в канонической форме записи:

.

Говорят, что ограничение ЗЛП имеет Предпочтительный вид, если при неотрицательности правой части () левая часть ограничения содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения-равенства – с коэффициентом, равным нулю.

Например, в системе ограничений

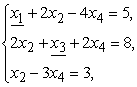
Первое и второе ограничения имеют предпочтительный вид, а третье – нет (предпочтительные переменные подчеркнуты).

Если каждое ограничение системы имеет предпочтительный вид, то система представлена в предпочтительном виде. В этом случае легко найти ее опорное решение. Предпочтительные переменные будут базисными, а остальные – свободными. Все свободные переменные нужно приравнять к нулю, тогда базисные переменные будут равны свободным членам.

Например, в системе ограничений:

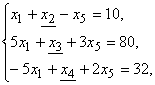
Предпочтительными (базисными) являются переменные свободными – переменные .

Приравниваем свободные переменные к нулю, тогда базисные переменные примут значения: , , .

Получим начальный опорный план .

< Предыдущая		Следующая >