07. Графический метод решения ЗЛП
Графическим методом можно решать любые задачи линейного программирования (ЗЛП) с двумя переменными (![]() =2), а также ЗЛП с
=2), а также ЗЛП с ![]() >2 переменными, если в ее канонической записи число неизвестных
>2 переменными, если в ее канонической записи число неизвестных ![]() и число линейно независимых уравнений
и число линейно независимых уравнений ![]() связаны соотношением
связаны соотношением ![]() .
.
Пример 6
Решим графически задачу ЛП, экономико-математическая модель которой составлена в примере 3.
![]() ;
;
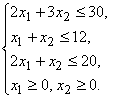 (2.10)
(2.10)
Вначале построим многоугольник решений или ОДР задачи (рисунок 1). Для этого в системе координат ![]() на плоскости изобразим граничные прямые:
на плоскости изобразим граничные прямые:
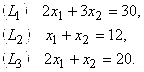
Затем определим, какую полуплоскость определяет соответствующее неравенство, подставив координаты какой-нибудь точки, например, начала координат. Ограничения (2.10) означают, что ОДР лежит в I четверти системы координат ![]() . Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет многоугольник решений данной задачи (ОДР).
. Соответствующие полуплоскости на рисунке показаны стрелками. Пересечение указанных полуплоскостей и определяет многоугольник решений данной задачи (ОДР).
Для того чтобы построить прямую ![]() , строим направляющий вектор
, строим направляющий вектор ![]() , который перпендикулярен прямой Z. Прямая, проходящая через начало координат и перпендикулярная вектору
, который перпендикулярен прямой Z. Прямая, проходящая через начало координат и перпендикулярная вектору ![]() , и будет прямая Z = 0. Затем прямую Z = 0 перемещаем параллельно самой себе в направлении вектора N По многоугольнику решений (ОДР) (рисунок 1). Последняя точка соприкосновения прямой Z = 0 с ОДР и есть оптимальное решение.
, и будет прямая Z = 0. Затем прямую Z = 0 перемещаем параллельно самой себе в направлении вектора N По многоугольнику решений (ОДР) (рисунок 1). Последняя точка соприкосновения прямой Z = 0 с ОДР и есть оптимальное решение.
Вектор ![]() указывает направление возрастания целевой функции Z. Оптимальное решение ЗЛП может достигаться лишь в точках, принадлежащих границе многоугольника решений. В нашем примере, как видно из рисунка 1, функция Z принимает максимальное значение в точке
указывает направление возрастания целевой функции Z. Оптимальное решение ЗЛП может достигаться лишь в точках, принадлежащих границе многоугольника решений. В нашем примере, как видно из рисунка 1, функция Z принимает максимальное значение в точке ![]() . Точка
. Точка ![]() лежит на пересечении прямых
лежит на пересечении прямых ![]() и
и ![]() . Для определения ее координат необходимо решить систему уравнений:
. Для определения ее координат необходимо решить систему уравнений:

Рисунок 1
Откуда ![]() . Это и есть оптимальный план задачи. Подставив значение
. Это и есть оптимальный план задачи. Подставив значение ![]() и
и ![]() в целевую функцию Z, получаем
в целевую функцию Z, получаем
![]() .
.
Таким образом, для того чтобы получить максимальную прибыль в размере 56 ден. ед., необходимо запланировать выпуск 8 ед. продукции вида П1 и 4 ед. продукции П2.
| < Предыдущая | Следующая > |
|---|
