6.1. Несобственные интегралы, зависящие от параметра
Пусть![]() – замкнутое, регулярное, измеряемое по Жордану множество.
– замкнутое, регулярное, измеряемое по Жордану множество. ![]() ;
;
![]() определена при
определена при ![]() .
.
Пусть кроме функции F задана функция ![]() , G – интегрируемая функция на множестве D. Рассмотрим следующий интеграл:
, G – интегрируемая функция на множестве D. Рассмотрим следующий интеграл: ![]() .
.
Определение: Пусть ![]() и пусть для каждого
и пусть для каждого ![]() сходится несобственный интеграл
сходится несобственный интеграл ![]() , тогда говорят, что этот интеграл сходится поточечно на множестве A.
, тогда говорят, что этот интеграл сходится поточечно на множестве A.
Определение: Пусть ![]() . Пусть для каждого
. Пусть для каждого ![]() можно указать такую окрестность
можно указать такую окрестность ![]() точки
точки ![]() , что для каждого
, что для каждого ![]() и для каждого множества A, лежащего в пересечении
и для каждого множества A, лежащего в пересечении ![]() и если A – измеримо по Жордану, то сходится несобственный интеграл
и если A – измеримо по Жордану, то сходится несобственный интеграл ![]() , причем
, причем  . Будем говорить, что несобственный интеграл
. Будем говорить, что несобственный интеграл ![]() сходится равномерно по Y в точке
сходится равномерно по Y в точке ![]() .
.
Замечание: Если несобственный интеграл ![]() Сходится равномерно по Y в точке
Сходится равномерно по Y в точке ![]() , то можно указать такую окрестность
, то можно указать такую окрестность ![]() точки
точки ![]() , что данный несобственный интеграл сходится поточечно к
, что данный несобственный интеграл сходится поточечно к ![]() .
.
Теорема: Пусть ![]() непрерывно зависит от X и Y при
непрерывно зависит от X и Y при ![]() . Пусть G – интегрируемая функция по X на D. Пусть
. Пусть G – интегрируемая функция по X на D. Пусть ![]() сходится равномерно по Y в точке
сходится равномерно по Y в точке ![]() . Обозначим
. Обозначим ![]() . Тогда интеграл I непрерывен в точке
. Тогда интеграл I непрерывен в точке ![]() .
.
Док-во: Фиксируем ![]() . Выберем окрестность
. Выберем окрестность ![]() точки
точки ![]() так, что
так, что ![]() – множество, измеримое по Жордану и так, что сходится интеграл
– множество, измеримое по Жордану и так, что сходится интеграл ![]() при
при ![]() , тогда:
, тогда:
1. ![]() – окрестность, измеримое по Жордану множество, а D – замкнутое, измеримое по Жордану множество.
– окрестность, измеримое по Жордану множество, а D – замкнутое, измеримое по Жордану множество.
2. ![]() непрерывно зависит от X и Y при
непрерывно зависит от X и Y при ![]() .
.
3. ![]() .
.
Согласно теореме о непрерывной зависимости собственного кратного интеграла от параметра ![]() непрерывно зависит от
непрерывно зависит от ![]() . Тогда можно указать такую окрестность
. Тогда можно указать такую окрестность ![]() точки
точки ![]() , что
, что ![]() .
.
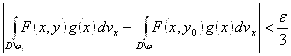


![]() , ч. т.д.
, ч. т.д.
Теорема (признак сравнения): Пусть F – непрерывная при ![]() функция, G – интегрируемая функция. Пусть
функция, G – интегрируемая функция. Пусть 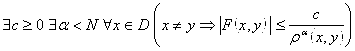 . Тогда для каждого
. Тогда для каждого ![]() интеграл
интеграл ![]() – сходится равномерно по Y в точке
– сходится равномерно по Y в точке ![]() .
.
Док-во N=3 (случай трехмерный): Пусть ![]() ,
, ![]() ,
, ![]() , при
, при ![]() . G – интегрируемая функция, а значит она ограниченная, следовательно, можно указать
. G – интегрируемая функция, а значит она ограниченная, следовательно, можно указать ![]() , что
, что ![]() при
при ![]() . Фиксируем
. Фиксируем ![]() . Рассмотрим
. Рассмотрим ![]() . Фиксируем
. Фиксируем ![]() так, чтобы множество A было множеством, интегрируемым по параметру Жордана,
так, чтобы множество A было множеством, интегрируемым по параметру Жордана, ![]() . Фиксируем
. Фиксируем ![]() точку Y в нашем шаре. Заметим,
точку Y в нашем шаре. Заметим, ![]() при
при ![]() . Согласно признаку сравнения для кратных несобственных интегралов при
. Согласно признаку сравнения для кратных несобственных интегралов при ![]() несобственный интеграл
несобственный интеграл ![]() – сходится.
– сходится.  . Заметим, что множество A гарантированно будет лежать в нашем шаре:
. Заметим, что множество A гарантированно будет лежать в нашем шаре: ![]() , следовательно, получаем:
, следовательно, получаем: 
![]()
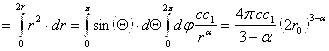 . Фиксируем
. Фиксируем ![]() и выберем
и выберем 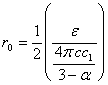 , тогда
, тогда  при
при ![]() , ч. т.д.
, ч. т.д.
Теорема (о дифференцировании): Пусть F – непрерывная функция при ![]() , а Y – интегрируемая функция. Пусть
, а Y – интегрируемая функция. Пусть ![]() , а несобственный интеграл
, а несобственный интеграл ![]() сходится поточечно на
сходится поточечно на ![]() , где
, где ![]() – некоторая окрестность точки
– некоторая окрестность точки ![]() . Пусть
. Пусть ![]() – непрерывна при
– непрерывна при ![]() . Пусть
. Пусть ![]() Сходится равномерно по Y в точке
Сходится равномерно по Y в точке ![]() , тогда:
, тогда:
1. ![]() имеет
имеет ![]() при
при ![]() .
.
2. 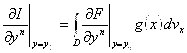 .
.
| < Предыдущая | Следующая > |
|---|