5.3. Интегралы Эйлера

Рассмотрим интеграл 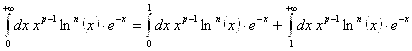. Рассмотрим первый интеграл. Пусть . Фиксируем . Рассмотрим предел следующей функции:

.

Причем, . Согласно признаку сравнения Сходится абсолютно. Пусть , тогда

.

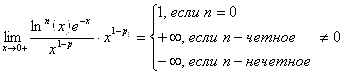Т. к. , то по признаку сравнения расходится.

Фиксируем . Пусть , тогда мы можем записать:

.

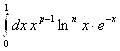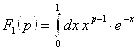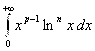Но интеграл по признаку Вейерштрасса сходится равномерно по P на сегменте . при , следовательно, – бесконечно гладкая на , причем . Интеграл сходится при всех P, сходится равномерно на . , следовательно, – бесконечно гладкая на и . Интеграл сходится при , расходится при и сходится равномерно на . Обозначим 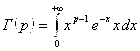– бесконечного дифференциала на . 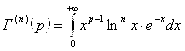- гамма-функция Эйлера (интеграл Эйлера).

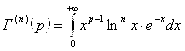
Признаки приведения

1. .

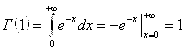2. .

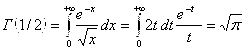3. (Формула приведения) Пусть , тогда . . Пусть – ее можно аналитически продолжить на комплексную плоскость, причем полюсами будут все целые точки отрицательной полуоси.

Формула дополнения

Пусть , тогда

Формула Стирлинга

Пусть , тогда

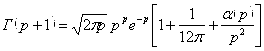
при .

Пусть 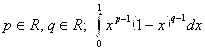– интеграл Эйлера первого рода, он сходится при , расходится при или , сходится равномерно на , где .

, при – -функция Эйлера.

. Тогда мы можем записать:

.

.

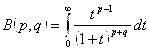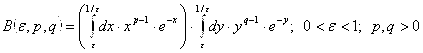
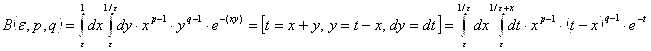
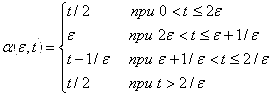
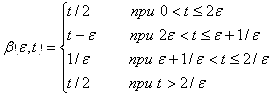
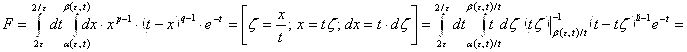
При :

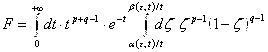, но Непрерывно зависят от и T при . Согласно теореме о непрерывной зависимости собственного интеграла от параметра непрерывно зависят

. Но также:

. Тогда получается:

. По признаку Вейерштрасса интеграл 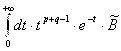сходится равномерно по на полупрямой :

– непрерывно зависит от .

Тогда , ч. т.д.

< Предыдущая		Следующая >