3.1. Равномерная сходимость функциональной последовательности и рядов

Пусть Сходится на Х к . Сходимость в точке X означает, что . В нашем случае, вообще говоря N Зависит от E и от Х.

Определение: Говорят, что функциональная последовательность сходится равномерно на множестве Х, если: (один и тот же для всех ) такой, что и .

Обозначения: на Х.

Геометрическая иллюстрация равномерной сходимости.

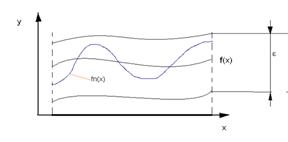
С геометрической точки зрения неравенство означает, что при График любой функции будет лежать в E-окрестности графика функции .

1) Сходится ли равномерно последовательность к функции на полуинтервале ?

2) Сходится ли равномерно функциональная последовательность на сегменте ?

Сформулируем эквивалентные определения равномерной сходимости что функциональной последовательности.

Определение: Функциональная последовательность называется равномерно сходящейся на множестве Х, если при , т. е. .

Определение: Говорят, что функциональный ряд сходится равномерно к функции на множестве Х, если последовательность его частичных сумм сходится равномерно к функции при на множестве Х. Иными словами, это означает что такой, что выполняется условие .

Пример 1: . Рассмотрим разность . Рассмотрим теперь супремум этого выражения: 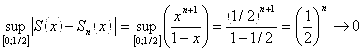при , следовательно, данный ряд сходится равномерно к своей сумме на сегменте множества X.

Примечание: Рассмотрим тот же ряд, но в случае, когда множество X принимает значения .

, следовательно, данная последовательность расходится на множестве X.

< Предыдущая		Следующая >