1.4. Поверхностный интеграл второго рода

Предположим, что задана полная, кусочно-гладкая, ориентированная поверхность. Создадим для поверхности Ф поле нормалей . Пусть на поверхности Ф заданы функции P(M), Q(M), R(M). Разобьем Ф на N полных квадрируемых поверхностей . Выберем , . Составим интегральную сумму:

Определение: Будем говорить, что I – это предел интегральной суммы при , если можно указать такое :

Если I является пределом интегральных сумм, то говорят, что I – поверхностный интеграл второго рода векторного поля поверхности Ф.

Рассматривают также частные интегралы второго рода:

Пусть G – регулярное, замкнутое, ограниченное и квадрируемое множество на плоскости. Предположим, что на множестве G задана вектор-функция , такая, что она задает гладкую поверхность Ф.

Теорема: Если функции P, Q и R непрерывны на поверхности Ф; , то существует интеграл второго рода I, причем выполняется равенство:

Док-во:

, ч. т.д.

Рассмотрим явно заданную поверхность . Радиус-вектор такой поверхности и его производные:

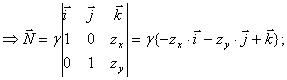
< Предыдущая		Следующая >