1.2. Поверхностные интегралы первого рода

Рассмотрим квадрируемую поверхность P. Рассмотрим разбиение этой поверхности P на квадрируемые части. Пусть на P задана непрерывная функция , . Составим интегральную сумму

Пусть .

Определение: Число I называется пределом интегральных сумм при , если для любого существует , такая, что для любого разбиения, для которого , и для любого выбора точек выполняется

Обозначается: .

Если такой предел существует, то он называется поверхностным интегралом первого рода, и имеют место следующие обозначения

или

Замечание: Поверхностный интеграл является обобщением двойного интеграла на тот случай, когда областью задания подынтегральной функции является криволинейная поверхность. Если , то соответствующее вычисление двойного интеграла дает нам площадь данной поверхности.

Теорема 1: Пусть поверхность P задана явным образом в замкнутой ограниченной области G. Пусть функция имеет в области непрерывные частные производные первого порядка. Эти требования необходимы для того, чтобы поверхность была гладкой. Пусть на поверхности P задана непрерывная функция F(M).Тогда поверхностный интеграл от функции F(X,Y,Z)вычисляются следующим образом:

Док-во: Рассмотрим разбиение поверхности и составим интегральную сумму

Указанная интегральная сумма соответствует поверхностному интегралу, находящемуся в левой части формулы (4). Рассмотрим интеграл из правой части формулы (4):

Воспользуемся формулой среднего значения:

Полученная сумма соответствует правой части формулы (4). Рассмотрим разность

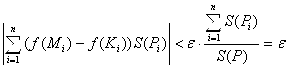
Таким образом, при указанном разбиении предельные значения левых и правых частей совпадают.

В том случае, когда поверхность задана параметрически, поверхностный интеграл вычисляется по формуле

< Предыдущая		Следующая >