05. Интерполяция алгебраическими многочленами. Многочлен Лагранжа
Если в качестве базисной взять систему степенных функций, то есть ![]() , то получаем задачу полиномиальной интерполяции:
, то получаем задачу полиномиальной интерполяции:
![]() (2.3.1)
(2.3.1)
Теорема 2.1. Существует единственный интерполяционный многочлен степени ![]() , Удовлетворяющий условиям (2.3.1).
, Удовлетворяющий условиям (2.3.1).
В качестве искомого многочлена возьмем многочлен степени ![]() вида
вида
![]() (2.3.2)
(2.3.2)
Таким образом, система функций, по которой строится интерполяционный многочлен, есть
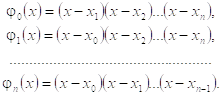
Для нахождения ![]() надо найти набор коэффициентов
надо найти набор коэффициентов ![]()
![]() . Не будем составлять и решать систему линейных уравнений вида (2.2.1), найдем коэффициенты иным способом.
. Не будем составлять и решать систему линейных уравнений вида (2.2.1), найдем коэффициенты иным способом.
Пусть ![]() , с учетом
, с учетом ![]() получим
получим
![]()
Аналогично, полагая ![]() и учитывая, что
и учитывая, что ![]() будем иметь
будем иметь
![]()
Если ![]() , то
, то ![]() Тогда сам многочлен
Тогда сам многочлен ![]() будет иметь вид
будет иметь вид
 (2.3.3)
(2.3.3)
Эта формула называется интерполяционной формулой Лагранжа. Приведем ее в сокращенной записи:
 (2.3.4)
(2.3.4)
Очевидно, ![]() представляет собой многочлен степени
представляет собой многочлен степени ![]() , удовлетворяющий условию
, удовлетворяющий условию
![]()
Таким образом, степень многочлена ![]() равна
равна ![]() , при
, при ![]() в формуле (2.3.4) обращаются в нуль все слагаемые, кроме слагаемого с номером
в формуле (2.3.4) обращаются в нуль все слагаемые, кроме слагаемого с номером ![]() , равного
, равного ![]() .
.
Выпишем отдельно многочлены Лагранжа первой и второй степени, ибо именно они чаще всего используются на практике.
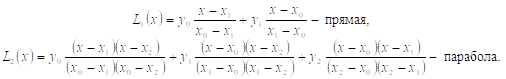 (2.3.5)
(2.3.5)
| < Предыдущая | Следующая > |
|---|