03. Погрешности функций

Пусть - функция - переменных, дифференцируемая в рассматриваемой области (например, на отрезке ).

Теорема 1.7. Для абсолютной погрешности значения справедлива следующая формула: .(1.4.1)

Доказательство

Вспомним сначала формулу Тейлора для функции нескольких переменных. Для функции одного переменного разложение в окрестности точки будет иметь вид

Для функции переменных форма записи формулы Тейлора остается точно такой же, если вместо производных записать дифференциалы соответствующих порядков:

Где, 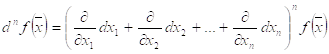. Например, для функции двух переменных

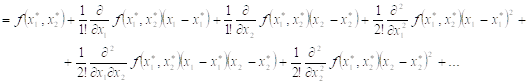
Отбрасывая все члены второго порядка и выше, получим

Таким образом, искомая формула сразу вытекает из формулы Лагранжа. Если достаточно мало, то для предельных значений погрешностей можно положить

Для относительных погрешностей тогда имеем следующие формулы:

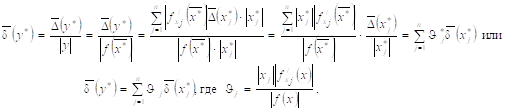(1.4.2)

I частный случай. Функция - функция одного переменного. Здесь следует положить , тогда . Для относительных погрешностей все аналогично:

.(1.4.3)

II частный случай. Функция - неявная. Этот случай отличается от исходного только формулой для нахождения частных производных:

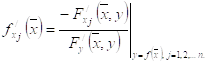
< Предыдущая		Следующая >