01. Погрешности чисел

Пусть - точное и неизвестное значение некоторой величины, а - ее известное приближенное значение.

Ошибкой (или погрешностью) приближенного значения числа называется разность . Количественной мерой ошибки является абсолютная погрешность

. (1.2.1)

По ней не всегда можно сделать правильное заключение о качестве приближения. Для этого вводится понятие относительной погрешности.

Относительной погрешностью приближенного значения числа Называется

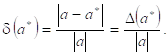(1.2.2)

Эта погрешность не зависит от масштаба величины единицы измерения. Непосредственное вычисление по формулам (1.2.1) и (1.2.2) невозможно, так как неизвестно. Часто задают величины 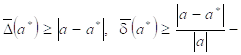верхние границы погрешностей и полагают

(1.2.3)

При записи приближенных чисел руководствуются следующими правилами. Пусть задано в виде конечной десятичной дроби .

Значащими цифрами числа называются все цифры в его записи, начиная с первой Ненулевой слева. Например,

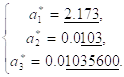Все значащие цифры подчеркнуты.

Значащую цифру числа Называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Пусть Тогда имеет три верные значащие цифры (они подчеркнуты). Если бы Было бы четыре верные значащие цифры. Число верных значащих цифр тесно связано с величиной относительной погрешности числа. Имеют место следующие результаты.

Теорема 1.1. Если содержит верных значащих цифр, то

Теорема 1.2. Для того чтобы число содержало верных значащих цифр, достаточно, чтобы

Теорема 1.3. Если имеет ровно Значащих цифр, то , То Есть

Эти теоремы позволяют оценивать по числу значащих цифр и наоборот. Например, если дано , то есть имеет шесть значащих цифр, то

При округлении возникает погрешность, называемая погрешностью округления. Существуют два способа округления.

1. Усечение – отбрасывание всех цифр, расположенных правее - ой значащей цифры. При этом погрешность не превышает (достигает) единицы того же разряда.

2. Округление по дополнению. Это следующее правило: если первая цифра слева от отбрасываемых меньше пяти, то лишнее просто отбрасывается, как при усечении; если же первая цифра слева от отбрасываемых больше или равна пяти, то в младший сохраняемый разряд добавляется единица. Абсолютная величина погрешности по дополнению не превышает половины единицы последней оставляемой значащей цифры.

Следующая >