10. Применение булевых функций для решения логических задач

В условии задачи выделяются простые высказывания и логичес­кие связки между ними. По условию задачи формируются истинные составные высказывания, которые затем соединяются знаком конъюнкции. Полученная истинная формула является символической записью условия задачи. Формула упрощается с помощью равносильных преобразований алгебры высказываний.

Пример. Определить, участвовал ли в соревновании Иванов, если известно, что:

1. Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал;

2. Если Иванов не участвовал, то Сидоров не участвовал.

Решение. Выделим в условии задачи простые высказывания: А =
= {Иванов участвовал}, В = {Петров участвовал}, С = {Сидоров участвовал}. Тогда первое условие задачи записывается в виде истинной формулы , второе условие – в виде истинной формулы . Соединим их знаком конъюнкции. Истинная формула является символической записью условия задачи. Упростим полученную формулу с помощью равносильностей алгебры высказываний теоремы 1.1 (см. пункт 1.3):

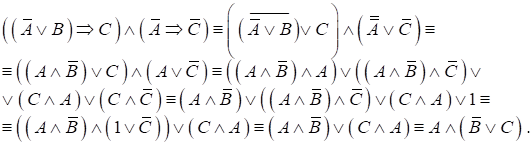
Так как упрощённая формула принимает значение «истина», то высказывания А и принимают значение «истина». Значит, Иванов участвовал в соревновании. □

Задачи и упражнения

1.36. Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что преступники скрылись на синем «Бьюике», Джонс сказал, что это был черный «Крайслер», а Смит утверждает, что это был «Форд Мустанг» и ни в коем случае не синий. Стало известно, что, желая запутать следствие, каждый из них указал правильно либо только марку машины, либо только ее цвет. Какого цвета и марки был автомобиль?

1.37. На вопрос, какая завтра будет погода, синоптик ответил:

1) если не будет ветра, то будет пасмурная погода без дождя;

2) если будет дождь, то будет пасмурно и без ветра;

3) если будет пасмурная погода, то будет дождь и не будет ветра.

С помощью алгебры логики определите погоду на завтра.

1.38. Известно, что если математическую логику изучал Василий, то ее изучал и Пётр. Неверно, что если Николай изучал логику, то её изучал и Пётр. Установите, кто из них изучал математическую логику.

1.39. Студенты второго курса Алексей, Борис, Владимир и Глеб сдавали экзамен по дискретной математике. Определите, кто из них сдал экзамен, если известно, что:

1) если Алексей сдал, то Борис тоже сдал;

2) если Борис сдал, то Владимир сдал или Алексей не сдал;

3) если Глеб сдал, то Алексей сдал и Владимир не сдал;

4) если Глеб сдал, то Алексей тоже сдал.

Вопросы для самоконтроля

1. Сформулируйте алгоритм составления формул алгебры высказываний.

2. Сформулируйте алгоритм проверки равносильности формул алгебры высказываний.

3. Укажите сходство и различие понятий «тавтология» и «противоречие».

4. Приведите примеры теорем математического анализа, имеющих конструкцию эквиваленции.

5. Приведите примеры теорем линейной алгебры, имеющих конструкцию импликации.

6. Составьте таблицы истинности для следующих логических операций:

1) Стрелка Пирса: ; 2) Штрих Шеффера: .

7. Сформулируйте определение формулы алгебры предикатов.

8. Образуйте из предикатов задачи 1.16 истинные высказывания.

9. Образуйте из предикатов задачи 1.16 ложные высказывания.

10. С помощью законов де Моргана получите отрицание высказывания, полученного в задаче 1.20.

11. Найдите СДНФ и СКНФ функции с помощью равносильностей алгебры высказываний.

12. Составьте все восемь высказываний, образованных путем применения кванторов к двухместному предикату по обеим переменным.

< Предыдущая