03. Равносильности алгебры высказываний
Определение. Две формулы называются Равносильными, если они одновременно истинны или одновременно ложны при любых значениях истинности входящих в них простых высказываний.
Для обозначения равносильности формул используется знак «![]() ».
».
Теорема 1.1. Для любых высказываний А, В И С справедливы следующие равносильности:
1) законы идемпотентности: ![]() ;
; ![]() ;
;
2) законы коммутативности:
![]() ;
; ![]() ;
; ![]() ;
;
3) законы ассоциативности:
![]() ;
; ![]() ;
;
![]() ;
;
4) законы дистрибутивности:
![]() ;
; ![]() ;
;
5) законы де Моргана: ![]() ;
; ![]() ;
;
6) закон снятия двойного отрицания: ![]() ;
;
7) законы исключения логических постоянных:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
8) законы поглощения: ![]() ;
; ![]() ;
;
9) законы, устанавливающие связь между логическими операциями:
![]() ;
;
![]() .
.
Равносильность утверждений теоремы проверяется с помощью Таблиц истинности.
Доказательство первого закона де Моргана. Составим общую таблицу истинности составных высказываний ![]() и
и ![]() .
.
|
А |
В |
|
|
|
|
|
|
И |
И |
И |
Л |
Л |
Л |
Л |
|
И |
Л |
И |
Л |
Л |
И |
Л |
|
Л |
И |
И |
Л |
И |
Л |
Л |
|
Л |
Л |
Л |
И |
И |
И |
И |
Её содержательная часть состоит из 4 строк и 7 столбцов.
Число строк равно 2N, N – Число простых высказываний в составном высказывании. Число столбцов таблицы определяется числом логических операций, используемых для формирования составных высказываний. В 1-м и 2-м столбцах записаны 4 различных набора истинностных значений Пары простых высказываний А и В. Остальные столбцы заполняются в соответствии с табл. 2.
Истинностные значения в 4-м и 7-м столбцах таблицы совпадают. Значит, ![]() ■
■
Перечисленные равносильности теоремы 1.1 используются для упрощения формул алгебры высказываний. Операции импликации и эквиваленции заменяются операциями дизъюнкции и конъюнкции, а отрицание относится к элементарным высказываниям.
Пример. Упростить формулу ![]() , используя равносильности алгебры высказываний.
, используя равносильности алгебры высказываний.


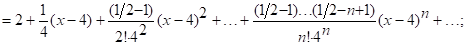
![]()
![]()
![]()
![]()
![]()
![]() .□
.□
Теорема 1.2. Всякая формула алгебры высказываний заменима формулой, содержащей только две операции – дизъюнкцию и отрицание или конъюнкцию и отрицание.
Например, 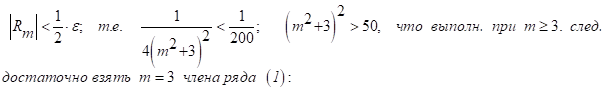 .
.
Задачи и упражнения
1.10. Определите среди следующих последовательностей формулы алгебры высказываний. Ответ обоснуйте.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() .
.
1.11. Докажите закон коммутативности дизъюнкции двух высказываний.
1.12. Проверьте по таблице истинности равносильность формул ![]() и
и ![]() .
.
1.13. Упростите формулу ![]() , используя равносильности алгебры высказываний.
, используя равносильности алгебры высказываний.
| < Предыдущая | Следующая > |
|---|