02.1. Понятие как результат обобщения

Отображение внешнего мира человеком начинается с чувственного познания, когда предметы и явления предстают перед ним как объекты непосредственного, живого созерцания. На этой ступени важная роль принадлежит органам чувств, с помощью которых информация извне поступает в мозг. В результате анализа и переработки полученной информации возникают: во-первых, ощущения, которые отображают отдельные свойства конкретных вещей (цвет, запах, твердость и т. п.); во-вторых, восприятия, в чувственной форме выражающие эти вещи целиком, т. е. как совокупность взаимосвязанных свойств; в-третьих, представления, когда вещь осознается без непосредственного ее восприятия. Поэтому представления занимают промежуточное положение между чувственным и рациональным познанием, так как они опираются прежде всего на память о тех впечатлениях, которые сохранились от непосредственного созерцания вещи. Но уже здесь происходит некоторое отдаление и отвлечение от второстепенных, несущественных черт и деталей вещи.

Переход от чувственного к рациональному познанию опирается прежде всего на процессы Абстрагирования и Обобщения. С помощью абстрагирования мы отвлекаемся от несущественных, неосновных, второстепенных свойств и отношений. Выделенные таким образом свойства и отношения являются общими для изучаемых классов вещей.

Понятие как раз и является той основной формой мышления, посредством которой мы выделяем определенные классы вещей и отличаем их друг от друга. Следовательно, понятие выступает, во-первых, как результат абстракции, т. е. мысленного выделения существенных свойств вещей от несущественных, главных – от второстепенных, а, во-вторых, как обобщение этих существенных свойств в едином понятии.

Обобщение заключается в отвлечении от всех индивидуальных различий внутри класса изучаемых объектов, например в понятии "студент" мы не обращаем внимания на его специальность, успеваемость, национальность и другие конкретные особенности.

Таким образом, Понятие можно определить как результат абстрагирования, выделения определенных классов предметов с помощью обобщения указанных предметов посредством их отличительного или существенного признака. Термин "признак" обозначает выраженные в понятии Свойства и Отношения реальных вещей.

Наиболее знакомыми и привычными для нас являются свойства, поэтому классическая логика ориентировалась на свойства вещей. Но между вещами существуют также разнообразные отношения, которые выражаются с помощью понятий. В современной логике их называют Предикатами (лат. praedicatum – логическое сказуемое суждения), причем свойства обозначаются одноместными предикатами, а отношения – многоместными предикатами.

Содержание и объем понятия

Прежде чем приступить к подробному анализу понятия, обратим внимание на различие между реальным предметом (вещью, явлением, процессом) и предметом мысли. Очевидно, что в понятии как форме мысли мы имеем дело с отображением реальных, объективных свойств. Следовательно, реальный предмет и предмет мысли принадлежат к разным областям действительности: первый – к миру объективному, существующему независимо от человека, второй – к субъективному миру познающего лица. Но это различие не исключает связи между ними. Если в наших понятиях мы будем адекватно отображать свойства и отношения вещей, то они будут давать нам верное знание о действительности.

Поскольку мы отличаем одни классы вещей от других, то для характеристики понятия основное значение приобретает его содержание.

Под Содержанием понятия подразумевают совокупность отличительных признаков предмета мысли. Так, в математике мы отличаем квадраты от ромбов и прямоугольников на том основании, что у ромбов стороны равны, но углы не равны, а у прямоугольников углы равны, но стороны не равны.

Обычно Понятие определяют как форму мысли, в которой отображаются существенные признаки изучаемых предметов. Однако заранее нам не известно, в какой мере те или иные признаки являются существенными. На деле это выявляется лишь в процессе исследования, особенно в научном познании. Поэтому целесообразно, на наш взгляд, говорить об отличительных признаках, с помощью которых мы можем различать разные классы предметов. Кроме того, для решения одних задач и проблем целесообразно считать существенными одни признаки, для решения других – иные. Например, хотя равносторонние и равноугольные треугольники составляют один и тот же класс, но содержание и смысл этих понятий различны, ибо в первом случае речь идет о сторонах треугольника, а во втором – об его углах.

Объем понятия можно определить как класс или множество тех предметов, которые обладают отличительными или существенными признаками, общими для них всех. Термин "класс" чаще всего употребляется в логике, в математике предпочитают говорить о Множествах. Но в данном случае мы не будем проводить между ними различия.

Множество (или класс) состоит из элементов, которые объединяются в целое по некоторым отличительным признакам. Так, объем понятия "первые три четных числа" будет состоять из чисел 2, 4 и 6, а объем всех четных чисел содержит бесконечное количество элементов. Общим признаком для любого четного числа является делимость на 2. Поскольку все четные числа составляют бесконечное множество, то в этом множестве можно выделить самые разнообразные подмножества, например подмножество четных чисел, делящихся на 3, 5, 7, и т. д.

Как мы убедимся в дальнейшем, операции над понятиями связаны с действиями над их объемами. Это же относится и к делению понятий на общие, единичные и нулевые. Если множество, представляющее объем понятия, состоит из многих или бесконечного числа элементов, то оно называется Общим. Примером может служить понятие "планеты Солнечной системы", содержащее конечное число элементов. Объем понятия "четное число", как мы видели, состоит из бесконечного числа элементов. Иногда понятие с бесконечным объемом называют Универсальным, чтобы отличить его от понятий, содержащих хотя и большое, но конечное число элементов. К Единичным относятся понятия, объем которых состоит из одного-единственного элемента. Часто такие понятия называют просто Описаниями, например выражения "самая высокая гора в Европе", "самая протяженная река в мире" и т. п. являются такими понятиями-описаниями. Наконец, к Нулевым понятиям относят те, объемы которых не содержат ни одного элемента, например понятие "вечный двигатель".

Рассмотрим теперь, как связаны между собой содержание и объем понятия.

Закон обратного отношения между объемом и содержанием понятия

Отношение между объемом и содержанием понятия было сформулировано в виде закона еще в XVII в. (логике Пор-Рояля). Коротко его можно выразить так: чем богаче содержание понятия, тем уже его объем и, наоборот, чем беднее содержание понятия, тем шире его объем. Например, содержание понятия четного числа богаче понятия натурального числа. Поэтому объем четного числа уже объема натурального числа. Аналогично этому содержание понятия "металл" богаче понятия "химический элемент" и, следовательно, объем понятия "металл" уже объема понятия "химический элемент". Обратите внимание, что закон обратного отношения применим к понятиям, находящимся друг к другу в отношении "частного" к "общему" или, точнее, "вида" и "рода".

Четные числа, как известно, составляют специфический вид натуральных чисел, а последние по отношению к ним являются родом. Точно так же металлы составляют часть или вид среди общего рода химических элементов. Термины "шире" и "уже", "богаче" и "беднее" употребляются при формулировке закона для краткости. Более развернуто они означают, что содержание будет богаче, если оно включает большее количество отличительных или существенных признаков. Объем соответственно считается более узким, если он содержит меньшее количество элементов.

Более точная формулировка закона обратного отношения между содержанием и объемом понятия может быть дана в таком виде: если объем одного понятия составляет часть другого, имеющего тот же род, то содержание второго составляет часть содержания первого понятия, и наоборот, когда содержание одного понятия есть часть содержания другого, тогда объемы понятий находятся в обратном отношении.

Несмотря на свою очевидность, этот закон не раз оспаривался в истории философии и методологии науки. Еще совсем недавно он подвергался критике сторонниками диалектической логики.

Какие доводы выдвигаются против закона обратного отношения между содержанием и объемом понятия?

Поскольку прогресс науки приводит к образованию новых, более общих и глубоких теорий, постольку эти понятия и теории не могут рассматриваться как более бедные по содержанию, считают критики данного закона. Другие идут еще дальше и заявляют, что такие общие понятия содержат все богатство особенного и единичного. Но эти доводы не выдерживают критики, во-первых, потому, что более общие понятия хотя и могут быть более глубокими, но они не могут сохранять в своем содержании специфические особенности менее общих и тем более единичных понятий. Другое дело, что в сочетании с той информацией, которая содержится в таких понятиях, более общие понятия дают более глубокое объяснение изучаемых явлений. Во-вторых, критики закона обратного отношения не учитывают тот факт, что процесс познания идет не только от частного к общему, от конкретного к абстрактному, но и в обратном направлении – от абстрактного к конкретному знанию. Абстракции создаются именно для того, чтобы глубже понять конкретную действительность, а это становится возможным только в единстве более общих и менее общих понятий. В-третьих, если бы критики закона были правы, тогда не стоило сохранять менее общие понятия и теории, но характерная особенность научного познания состоит именно в преемственности развития, сохранении и удержании всего того ценного, что достигнуто на предшествующих этапах познания.

Отношения между понятиями

Определив объем понятия, можно рассмотреть, какие отношения могут существовать между различными их типами.

Отношение эквивалентности существует тогда и только тогда, когда объемы сравниваемых понятий полностью совпадают. Это означает, что отличительные или существенные признаки, присущие сравниваемым понятиям, принадлежат всем элементам множеств, составляющих их объемы. Так, понятие эквивалентности характеризует отношение между классами равносторонних и равноугольных треугольников, равноугольных ромбов и квадратов, равносторонних прямоугольников и квадратов. Легко убедиться, что, несмотря на отличительные признаки этих понятий, все они принадлежат к одному классу элементов, т. е. имеют тот же самый объем. Обратите внимание на то, что все перечисленные понятия оказываются эквивалентными только по объему, содержание же их различно. Так, признаки "иметь равные стороны" или "обладать равными углами" отличаются друг от друга по смыслу.

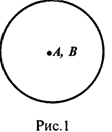
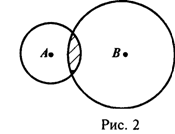
Отношение перекрещивания (частичного совпадения) Объемов понятий существует тогда и только тогда, когда часть объема одного понятия входит в объем другого, и в свою очередь часть объема второго понятия входит в объем первого. Таковы отношения между объемами понятий "студенты" и "спортсмены", "студенты" и "филателисты", ибо ясно, что не все студенты являются спортсменами или филателистами. Обычно для наглядного изображения отношений между объемами понятий употребляются диаграммы Л. Эйлера, в которых объем понятия представляется кругом. Поскольку у эквивалентных понятий объемы совпадают, то отношение между ними изображается одним кругом. В случае частичного совпадения объемов отношение изображается пересечением двух кругов. Если обозначить объем одного понятия через А, другого – через В, то графически отношения эквивалентности (рис. 1) и перекрещивания (рис. 2) можно представить соответствующими диаграммами.

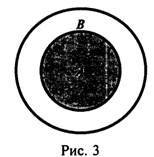
Отношение субординации (подчинение объемов) понятий существует тогда и только тогда, когда объем одного понятия полностью входит в объем второго. Понятие меньшего объема составляет часть, или, точнее, Вид понятия с большим объемом, который по отношению к нему называют Родом. На диаграмме Эйлера (рис. 3) это отношение изображается включением меньшего круга в больший.

Все перечисленные выше отношения имеют место между совместными понятиями, объемы которых либо совпадают, либо перекрещиваются, либо составляют часть другого.

Несравнимые («неположенные) понятия – это понятия, объемы которых либо полностью исключают друг друга, либо находятся в отношении противоречия друг другу. Так, объемы понятий "треугольник" и "растение" не содержат ни одного общего элемента, их пересечение – пусто. То же самое можно сказать о понятиях, которые употребляются в хорошо известном утверждении, характеризующем несравнимость: "В огороде бузина, а в Киеве дядька".

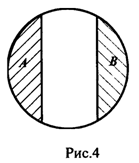
Особый интерес представляют понятия, объемы которых находятся в отношении контрарности (противности) друг другу, как, например, "белый" и "черный", "холодный", и "горячий", "длинный" и "короткий" и т. д., которые представляют собой свойства, расположенные на границе соответствующих множеств свойств. Между "белым" и "черным", "холодным" и "горячим" и т. д. располагаются промежуточные свойства. В силу этого объемы контрарных понятий занимают крайние положения на круговых диаграммах (рис. 4).

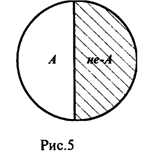
Отношение контрадикторности (противоречивости) между объемами понятий существует тогда, когда они, с одной стороны, отрицают друг друга, а с другой исчерпывают объем целого понятия (рис. 5).

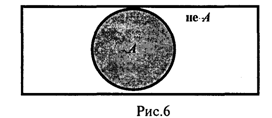
В языке противоречие выражается отрицательной частицей перед словом, выражающим свойство. Примерами могут служить свойства, выражающие такие понятия, как белый и не белый, холодный и не холодный, черный и не черный и т. п. На диаграмме (см. рис. 5) объемы таких понятий составляют две половины круга, хотя гораздо лучше представить объем положительного понятия кругом, а отрицательного – прямоугольником, в который входит этот круг, поскольку противоположное (отрицательное) понятие содержит обычно большее число элементов (рис.6).

Поскольку объемы понятий образуют классы (или множества) предметов, элементы которых обладают признаками, сформулированными в их содержании, то над этими классами (или множествами) можно производить определенные логические операции. Они тождественны операциям, которые изучаются в теории множеств.

Объединением классов (или множеств) называют класс, который содержит в своем составе все элементы, входящие в каждый отдельный класс. Если обозначить отдельные классы через А1, А2, А3,…, АN, То объединенное множество можно представить как дизъюнкцию (или логическое сложение) всех перечисленных классов (или множеств):

UАI = A1U A2U A3 … UAN.

Например, объединение плоских фигур будет состоять из класса треугольников, класса четырехугольников, окружностей и других фигур, класс деревьев – из классов хвойных, лиственных и других деревьев.

Пересечением (или Умножением) классов называется новый класс, который содержит в своем составе те и только те элементы, которые входят в каждый из отдельных классов. Иначе говоря, он содержит элементы, общие всем отдельным классам. Поэтому сама операция пересечения классов иногда называется Взятием их общей части. Обозначив отдельные классы через А1, А2, А3,…, АN, их пересечение можно представить в виде: ÙAI = A1, ÙA3,…, ÙАN, где знак л обозначает операцию пересечения, умножения или конъюнкции классов.

Обобщение и ограничение понятий

Под Обобщением понятий подразумевается операция перехода от понятий меньшего объема к понятиям большего объема, а под Ограничением – обратный процесс перехода от понятий большего объема к понятиям меньшего объема. Однако в отличие от предыдущего случая отношений понятий с фиксированными объемами, при обобщении и ограничении понятий происходит также изменение содержания понятий, поскольку при обобщении некоторые признаки исключаются, а при ограничении, наоборот, прибавляются. Это непосредственно следует из закона обратного отношения между объемом и содержанием понятия.

Обобщение понятий неразрывно связано с процессом абстрагирования, в результате чего отвлекаются от тех признаков, которые в ходе познания оказываются несущественными, и потому опускаются. Процесс ограничения связан с противоположным движением мысли, который называется Конкретизацией, или точнее Спецификацией. Только благодаря конкретизации общие понятия можно применять для исследования частных случаев.

Наиболее ясно обобщение и ограничение понятий прослеживается в математике, причем в чистой, (теоретической) математике преобладает процесс обобщения понятий, а в приложениях математики – их конкретизация.

Хотя с логической точки зрения такие обобщения понятий представляются вполне ясными и даже очевидными, но исторически новые понятия и основанные на них теории находили признание не сразу, не без борьбы мнений и конфликтов. Достаточно лишь отметить, например, с какими трудностями ученые столкнулись при обобщении понятия числа и введении понятий иррациональных и мнимых чисел, а в недалеком прошлом – понятий о неевклидовых пространствах и бесконечных множествах. В неменьшей степени конфликты сопровождали обобщения и введение новых понятий в астрономии мира, например, гелиоцентрической системы мира (вместо геоцентрической птолемеевой системы мира), в физике, биологии и других науках.

< Предыдущая		Следующая >