02. Постановки задачи линейного программирования
Общая задача линейного программирования (ОЗЛП) может быть сформулирована следующим образом: найти значения переменных Х1, Х2,…,Хn, максимизирующие линейную форму
![]() (x1,x2,…,xn) = c1x1+…+cnxn (3.1)
(x1,x2,…,xn) = c1x1+…+cnxn (3.1)
При условиях
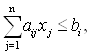 i = 1,…, m1 (m1 £ m) , (3.2)
i = 1,…, m1 (m1 £ m) , (3.2)
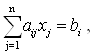 i = m1 + 1,…, m,
i = m1 + 1,…, m,
xj ³ 0, j = 1,…, p (p £ n) . (3.3)
Соотношения (3.2) и (3.3) будем называть соответственно функциональными и прямыми ограничениями задачи линейного программирования (ЗЛП).
Значения переменных Хj (j = 1, 2,…, n) можно рассматривать как компоненты некоторого вектора ![]() = (Х1, Х2,…, Хn) пространства Еn.
= (Х1, Х2,…, Хn) пространства Еn.
Определение. Планом, или допустимым решением, задачи линейного программирования будем называть вектор ![]() пространства Еn, компоненты которого удовлетворяют функциональным и прямым ограничениям задачи.
пространства Еn, компоненты которого удовлетворяют функциональным и прямым ограничениям задачи.
Множество всех планов задачи линейного программирования (3.1) – (3.3) будем обозначать Р.
Теорема 3.1. Множество планов Р задачи линейного программирования (ЗЛП) есть замкнутое выпуклое множество.
Множество Р может быть как ограниченным, так и неограниченным, кроме того оно может оказаться пустым.
Напомним, что множество точек Р пространства En есть выпуклое множество, если вместе с любыми двумя его точками ![]() и
и ![]() Ему принадлежит и любая выпуклая линейная комбинация этих точек, то есть если
Ему принадлежит и любая выпуклая линейная комбинация этих точек, то есть если ![]() ,
,![]() , то и любая точка
, то и любая точка
![]() , 0 ≤ λ ≤ 1
, 0 ≤ λ ≤ 1
Также принадлежит множеству Р.
Множество точек ![]() = (Х1, Х2,…, Хn) пространства En, компоненты которых удовлетворяют условию
= (Х1, Х2,…, Хn) пространства En, компоненты которых удовлетворяют условию
C1X1 + C2X2 +…+ CnXn = b,
Называется гиперплоскостью пространства En.
Множество точек ![]() = (Х1, Х2,…, Хn) пространства En, компоненты которых удовлетворяют условию
= (Х1, Х2,…, Хn) пространства En, компоненты которых удовлетворяют условию
C1X1 + C2X2 +…+ CnXn ≤ b ( ≥ b ),
Называется полупространством пространства En.
Очевидно, что гиперплоскость и полупространство являются выпуклыми множествами пространства En.
Напомним, что точка ![]() Выпуклого множества К является крайней, если в К не существует таких точек
Выпуклого множества К является крайней, если в К не существует таких точек ![]() и
и ![]() ,
, ![]() ≠
≠![]() , что
, что
![]() , при некотором
, при некотором ![]() .
.
Геометрически это означает, что эта крайняя точка не может лежать внутри отрезка, соединяющего две точки выпуклого множества. Она лишь может быть одной из концевых точек этого отрезка.
Определение. План ![]() = (Х1*,…Хn*) будем называть решением задачи линейного программирования, или ее оптимальным планом, если
= (Х1*,…Хn*) будем называть решением задачи линейного программирования, или ее оптимальным планом, если
![]() .
.
Определение. Будем говорить, что задача линейного программирования разрешима, если она имеет хотя бы один оптимальный план.
| < Предыдущая | Следующая > |
|---|