Лекция 1

Цель лекции – дать классическое определение понятия вероятности события

План лекции

1. СЛУЧАЙНЫЕ СОБЫТИЯ

1.1 Операции над событиями и их определение

1.2 Алгебра событий

1.3 Уточнение определений и понятий

1.4 Классическая формулировка вероятности событий

Курс лекций состоит их двух разделов:

Теория вероятностей –

Случайные события

Случайные величины

Случайные векторы

Случайные процессы

Элементы математической статистики

Теория вероятностей (ТВ) - это наука, которая занимается изучением случайных массовых явлений. Основным понятием в этой науке является вероятность события, которая представляет собой численную меру возможности появления этого события (см. приложение 1 лкц 01-02п).

Математическая статистика (МС) - это наука, которая занимается сбором, обработкой и описанием данных опыта с целью выявления теоретических закономерностей, которым подчиняются случайные явления. МС является источником и базой ТВ (см. приложение 2 лкц 01-02п).

1. СЛУЧАЙНЫЕ СОБЫТИЯ

В теории вероятностей всякое явление, о котором можно говорить, что оно происходит или не происходит, называется событием.

Случайным событием называется событие, которое при определенном комплексе факторов может произойти, а может не произойти. Принято говорить “ произведено испытание ” в том случае, если такой комплекс факторов реализован.

Достоверные события - это события, которые при определенном комплексе факторов обязательно происходят.

Невозможным событием называется событие, которое при определенном комплексе факторов обязательно не происходит.

Несовместные события - два события несовместны, если появление одного исключает появление другого (См. также п. 1.3 ).

Используются следующие обозначения :

Случайные события - А, В, С... или А1, А2, А3…

Достоверные события – U.

Невозможные события – V.

Цель лекции — дать формулировку понятию вероятности.

1.1. Операции над событиями и их определение

При вычислениях вероятности появления того или иного события часто приходится рассматривать его как совокупность других событий. Таким образом, возникает необходимость производить преобразования, для чего устанавливают правила таких преобразований.

1. Если событие А происходит при появлении события В, то говорят, что В включает в себя А и записывают:

2. Если , то А=В.

3. Событие называется противоположным событию А, если оно состоит в том, что событие А не происходит.

4. Произведением событий А и В называют событие С=А´В , которое означает, что А и В происходят одновременно

5. Суммой 2-х событий А и В называют событие С=А+В, которое означает, что происходит либо событие А, либо событие В, либо А и В одновременно.

А+В ' А×В;

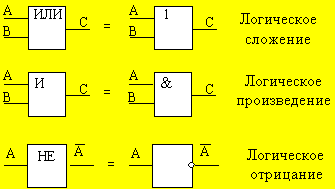
В вычислительной технике существуют элементы, которые выполняют указанные операции над сигналами.

1.2. Алгебра событий

Алгебра событий устанавливает правила, по которым можно осуществлять операции над событиями:

1. А+В=В+А	7. А×В=В×А	13. U=
2. А+U=U	8. А×U=А	14.
3. А+V=A	9. А×V=V	15. =А
4. А+А=A	10. А×А=A	16.
5. А+=U	11. А×=V	17.
6.	12. (А×В)×С=(А×С)×В

Пример упрощающего преобразования :

А+А×В = А×U+A×B = A×(U+B) = A×U = A.

1.3. Уточнение определений и понятий

Выше была дано определение понятия о несовместных событиях. Это понятие можно сформулировать, используя алгебру событий.

1. События А и В несовместны, если

А×В=V. (См. определение выше)

2. События А1, А2, …, Аn называются несовместными попарно, если

АiВj=V, где i, j = 1,2,3, …, n; i ¹ j.

3. События А1, А2, …, Аn называются несовместными попарно и в совокупности, если произведение любого события на любую совокупность оставшихся есть событие невозможное, то-есть

Аi×Rn-1=V,

Где - Rn-1 - любая совокупность оставшихся событий, i = 1,2,3, …, n.

4. События А1, А2, …, Аn называются полной группой событий, если

А1 + А2 + …+ Аn = U.

Для полной группы событий появление хотя одного из них является достоверным событий.

5. Если в полной группе событий А1, А2, …, Аn все они несовместны попарно и в совокупности, то такие события называются элементарными случаями (ЭС).

6. События называются равновозможными, если условия появления каждого из них одинаковы.

7. Те элементарные случаи, при которых событие А появляется, называются случаями, благоприятствующими событию А.

1.4. Классическая формулировка вероятности событий

Вероятностью Р(А) появления события А называют отношение числа m элементарных случаев, благоприятствующих событию А, к общему числу n всех элементарных равновозможных случаев:

, 0 ≤ ≤ 1.

Если событие невозможно, то

Р(V) = 0 .

Если событие достоверно, то

Р(U) = 1.

Если событие А таково, что вероятность его появления весьма мала - к примеру Р(А)=0,001 - , а событие В имеет вероятность появления близкую к 1 - примеру Р(В)=0,999 - , то событие А называется Практически невозможным, а событие В – Практически Достоверным.

Вероятность события, вычисленную с использованием классической формулировки, называют также математической вероятностью.

Недостатки классической формулировки очевидны. Они заключаются в том, что трудно, а в большинстве случаев невозможно представить событие как совокупность элементарных равновозможных случаев.

Пример алгебраических преобразований:

Доказать: ;

Прибавим к обеим частям А+В:

По определению

Другой пример доказательства правила 16

Добавим к обеим частям равенства сумму А+В . Согласно правилам получим

Добавим к правой части полученного выражения произведение И сгруппируем

Согласно правилу 17

И таким образом правомерность правила 16 доказана

1 Приложение к Лекции 1

Можно привести пример относительно тех выводов, которые следуют из теории вероятности - пример расчета вероятности гибели слона в зоопарке окруженного Ленинграда. Он был убит на следующий день, хотя по расчету такая вероятность был очень и очень мала. Но не нулевая!!! Поэтому, если кто-то утверждает, что некоторое событие маловероятное, это не означает, что оно невозможное

2 Приложение к Лекции 1

В романе К. Симонова "Живые и мертвые" есть такая фраза : … война поделила их на живых и мертвых. Это вполне понятное и без математической статистики утверждение.

Известно уже из практики ведения войн, что наступающая сторона теряет убитыми и ранеными примерно треть личного состава. Этот факт известен и командирам и рядовым, поэтому можно понять настроение среди солдат перед началом наступления. Это неумолимая и нелицеприятная правда. От этого некуда деться, и вопрос только в том, кто из них третий.

В 70-х годах прошлого века вдруг начали рождаться дети с аномально короткими верхними конечностями (почти без предплечья). Наблюдения показали, что причиной было употребление женщинами нового снотворного. Таким образом, дети-инвалиды своей несчастной жизнью обязаны случаю, и трудно винить их матерей.

В настоящее время статистика наблюдений показывает, что ощутимые отклонения от нормы среди новорожденных за счет генетических ошибок наблюдается примерно один на тысячу. Достаточно твердо установлено, что количество таких ошибок возрастает на порядок, если женщина курит. И если все отмеченные выше ужасные последствия явилось следствием случайных причин, действие которых в отдельных случаях можно было бы избежать, то дико рисковать своим благополучием в угоду желанию иметь "имидж". Это хочется сказать тем девушкам, особенно миниатюрного телосложения, которые курят и при этом нерегулярно питаются. Попробуйте представить себя в роли матери ребенка-урода.

Настораживает, что количество курящих увеличивается. Настораживает потому, что никто сейчас не может предсказать как скажется такая массовость.

Следующая >