19. Нормальное распределение на плоскости
Нормальное распределение на плоскости – это нормальное распределение для системы двух случайных величин X и Y.
Нормальное распределение на плоскости задается плотностью
 .
.
Распределение зависит от пяти параметров: ![]() . Выясним их смысл. Для этого найдем плотности компонент X и Y:
. Выясним их смысл. Для этого найдем плотности компонент X и Y:
 ;
; 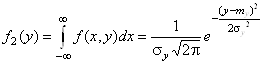
Cлучайные величины X и Y имеют нормальное распределение c параметрами ![]() и
и ![]() cоответственно. Cледовательно,
cоответственно. Cледовательно, ![]() .
.
Посчитаем ковариацию компонент X и Y.

Отсюда следует, что параметр R совпадает с коэффициентом корреляции X и Y:
![]() .
.
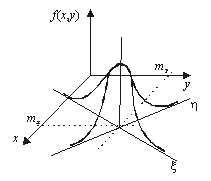 Геометрически плотность двумерного нормального закона представляет собой “холм”, вершина которого находится над точкой (
Геометрически плотность двумерного нормального закона представляет собой “холм”, вершина которого находится над точкой (![]() ). В сечении поверхности плотности плоскостями, параллельными оси
). В сечении поверхности плотности плоскостями, параллельными оси ![]() , получаются кривые, подобные гауссовым кривым. В сечениях плоскостями, параллельными плоскости XOY, получаются эллипсы. Уравнения эллипсов:
, получаются кривые, подобные гауссовым кривым. В сечениях плоскостями, параллельными плоскости XOY, получаются эллипсы. Уравнения эллипсов: 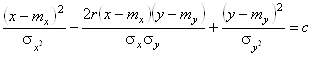 . Эти эллипсы называются эллипсами рассеивания, а оси этих эллипсов (общие для всех эллипсов) называются главными осями рассеивания (h и x).
. Эти эллипсы называются эллипсами рассеивания, а оси этих эллипсов (общие для всех эллипсов) называются главными осями рассеивания (h и x).
| < Предыдущая | Следующая > |
|---|