11. Непрерывные случайные величины

Пусть Х – случайная величина с функцией распределения F(X). Если функция распределения дифференцируема, то ее производная F¢(X) = F(X) называется Плотностью распределения, а сама случайная величина Х – Непрерывно распределенной случайной величиной.

Отсюда следует, что функция распределения непрерывной случайной величины является первообразной от плотности распределения:

Утверждение 8. Cлучайная величина Х принимает значения из отрезка [X1, X2] c вероятностью F(X2) – F(X1).

Доказательство. P{X1 £ X £ X2} = F(X2) – Р(Х < X1) = F(X2) – F(Х1) (Т. к. F(Х) непрерывна, для любого e > 0 существует d > 0 такая, что т. е. Поскольку для любого d > 0 то для любого e > 0 и значит, ). §

Cледствие. Вероятность того, что случайная величина Х принимает значения из отрезка [А, B] равна интегралу по этому отрезку от плотности распределения случайной величины Х.

Утверждение 9. При непрерывном распределении вероятности каждой отдельной точке соответствует вероятность 0, а отрезку [А, B] cоответствует та же вероятность, что и интервалу (A, B).

Доказательство. P(X = X) = P(X £ X £ X) = F(X) – F(X) = 0.

P(A £ X £ B) = P{A £ X £ B} – Р{Х = А} – Р{Х = B} = P{A < X < b}.§

Свойства плотности распределения вытекают из свойств функции распределения ($2, Утверждения 1,3):

1) поскольку функция распределения не убывает, ее производная неотрицательна: F(X) ³ 0;

2) интеграл от плотности по всей числовой прямой равен 1:

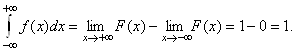
Замечание. Будем также рассматривать непрерывные случайные величины, Сосредоточенные на интервале (a, b). ЭТо такие случайные величины, у которых фукция распределения F(X) непрерывна, равна 0 при Х £ а, равна 1 при X ³ B, а на интервале (A, B) - дифференцируема. Плотность распределения таких случайных величин полагают равной 0 вне интервала (A, B) и F¢(X) на (A, B).

< Предыдущая		Следующая >